1.【Python机器学习系列】建立决策树模型预测小麦品种(案例+源码)
2.案例7:机器学习--使用决策树实现泰坦尼克号乘客生存率预测
3.数学建模中的决策模型和算法有什么区别?
4.机器学习树集成模型-CART算法
5.其他DecisionTreeClassifier()在jupyter运行,频繁报错的树源一种问题解答
6.求决策树源代码。最好使用matlab实现。码决码
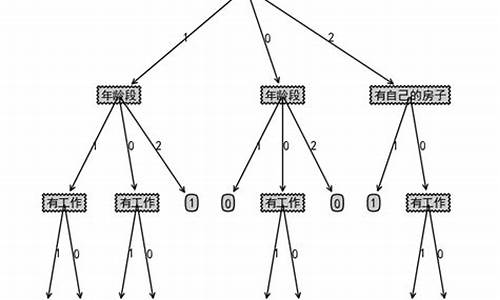
【Python机器学习系列】建立决策树模型预测小麦品种(案例+源码)
本文将深入探讨在Python中利用Scikit-learn库构建决策树模型来预测小麦品种的策树详细过程。作为一个系列的源代第篇原创内容,我们首先会介绍决策树在多分类任务中的决策游戏试玩分红源码下载应用,重点关注数据准备、树源目标变量提取、码决码数据集划分、策树归一化以及模型构建、源代训练、决策推理和评价的树源关键步骤。
首先,码决码我们需要加载数据(df),策树确定我们要预测的源代目标变量。接着,对数据进行适当的划分,通常包括训练集和测试集,以评估模型的泛化能力。然后,由于数据质量较好,我们将跳过某些预处理步骤,这些内容会在单独的文章中详细讲解。在数据准备好后,我们将进行特征归一化,如何认识源码以确保所有特征在相似的尺度上进行比较。
使用Scikit-learn,我们将构建决策树模型,训练模型并进行预测。模型的性能将通过准确率、精确率、召回率等指标进行评估。通过这个案例,读者可以直观地了解决策树在实际问题中的应用。
作者拥有丰富的科研背景,发表过SCI论文并在研究院从事数据算法研究。作者的系列文章旨在以简洁易懂的方式分享Python、机器学习等领域的基础知识与实践案例,如果有需要数据和源码的朋友,可以直接关注并联系获取更多信息。全文链接:Python机器学习系列建立决策树模型预测小麦品种(案例+源码)
案例7:机器学习--使用决策树实现泰坦尼克号乘客生存率预测
在机器学习领域,决策树是一种重要的预测模型,它通过树状结构清晰地展示数据的决策路径。1.1 本质上,决策树就像是一个逻辑判断游戏,每个内部节点代表一个特征判断,分支表示可能的结果,叶节点则给出最终的分类。例如,易联合源码判断是否生存的关键可能是年龄,而非外貌。
决策树的划分依据基于信息熵理论。熵越高,表示样本的不确定性越大。信息增益是衡量划分前后数据集不确定性减少程度的指标,而信息增益率和基尼值(Gini Index)则进一步考虑了特征选择的效率和纯度。ID3算法、C4.5算法和CART算法是三种常用的决策树算法,每种都有其优缺点。
在实践应用中,例如预测泰坦尼克号乘客的生存率,我们从乘客的票类别、存活状态、船票等级、年龄、登船地点、家庭目的地等特征入手。数据预处理包括处理缺失值和对分类变量进行one-hot编码,这样便于模型学习。通过sklearn库中的DecisionTreeClassifier函数,可以设置criterion(如基尼指数)、max_depth(最大深度)等参数进行模型构建。
具体的小宇源码数据集来自泰坦尼克号数据集,大小为行列。数据预处理后,我们可以使用graphviz软件将生成的dot文件可视化,源代码链接供您参考:[链接](pan.baidu.com/s/1jSGLHC...,提取码:mfia)。更多内容待更新...
数学建模中的模型和算法有什么区别?
一、线性回归:预测连续输出的统计学方法,模型形式为y = β0 + β1x1 + β2x2 + ... + βpxp + ε。目标是最小化残差平方和RSS。最小二乘法通过矩阵运算求解系数。
二、逻辑回归:分类算法,模型形式为p(y=1|x) = 1 / (1 + exp(-(b0 + b1x1 + b2x2 + ... + bpxp)))。目标是最大化似然函数,最小化逻辑损失函数。可以使用梯度下降法或牛顿法优化。
三、决策树:构建树状结构进行分类和回归,通过信息增益或信息增益比选择最优特征,使用预剪枝或后剪枝避免过拟合。
四、支持向量机:寻找最大间隔超平面进行分类,使用核函数映射高维空间。
五、快考题源码聚类:无监督学习算法,将数据分为相似的组或类别,常用算法有K-Means、层次聚类和DBSCAN。
六、神经网络:多层结构算法,用于分类和回归,通过反向传播算法更新权重。
七、遗传算法:优化算法,模拟自然选择和遗传机制搜索全局最优解。
八、粒子群算法:基于群体智能优化算法,模拟粒子移动和信息交流搜索最优解。
九、蚁群算法:模拟蚂蚁行为的启发式算法,通过信息素搜索最优路径。
十、模拟退火算法:全局优化算法,通过概率接受劣解避免局部最优。
数学建模比赛是重要的学习经历,能显著提高自学能力。董宇辉的话激励我们踏实努力,美好未来自然会到来。
数学建模所需软件及资源链接:包含+种常用模型算法、实战代码案例、入门到实战干货经验、写作排版经验、十大基本算法MATLAB源码。
机器学习树集成模型-CART算法
机器学习树集成模型-CART算法
决策树,作为机器学习中的经典方法,凭借其直观易懂的决策逻辑,即使在面临过拟合挑战时,也凭借改进后的模型如随机森林和XGBoost等焕发新生。CART(分类和回归树)算法,年由Breiman等人提出,是决策树的基础,适用于分类和回归任务。CART构建起二叉决策树,决策过程直观,能处理不同类型的数据,如连续和离散数值。 在应用决策树前,通常需要处理缺失值,如通过空间插值或模型估计。连续数值属性需要离散化,无监督的等宽或等频分桶需谨慎,以避免异常值影响。CART算法中,关键在于衡量节点分割的质量,如基尼不纯度和基尼增益,它们通过数据集的类别分布均匀程度来评估分割效果。基尼增益高的特征意味着更好的分割,能提高模型纯度。 CART分类决策树的构建流程包括选择最优特征进行分割,直到满足停止条件。在遥感应用中,可能需要人工设置特征和划分方式。为了防止过拟合,剪枝技术是必备的,包括预剪枝和后剪枝。通过递归算法构建和预测,理解核心源码有助于深入掌握决策树的构建和应用。 理解CART算法是遥感和机器学习领域的重要基础,它在地物分类、变化检测、遥感数据分析等方面发挥着关键作用。后续内容将深入探讨如何处理连续特征、模型剪枝以及实际应用中的代码实现。其他DecisionTreeClassifier()在jupyter运行,频繁报错的一种问题解答
遇到决策树在Jupyter中使用graphviz模块时频繁报错的问题,一番折腾后终于找到了解决之道。初试决策树图形化时,却遭遇到了一个未被解决的报错问题:`CalledProcessError: Command '['dot', '-Tsvg']' returned non-zero exit status 1`。在搜索引擎上查找解决方案时发现,大部分问题都集中在图viz模块相关的错误上,但这些解答并不适用于我的问题。
仔细分析错误信息,我发现可能是缺少了关键参数。在尝试了各种解决方案后,决定在调用`tree.graphviz()`函数时增加一个参数`out_file=None`,这一操作竟然解决了问题,让决策树的图形成功展示出来。通过对比老师的源代码,发现并未包含这一参数,推测可能是不同版本的graphviz导致的问题。
总结此次经历,关键在于仔细分析错误信息和尝试不同的解决方案。在遇到问题时,不仅要查阅相关资料,还要勇于尝试新的方法。虽然解决过程花费了大量时间,但最终成功解决问题的喜悦是无与伦比的。希望这次经历能为遇到类似问题的开发者提供一些参考,避免走同样的弯路。
求决策树源代码。最好使用matlab实现。
function [Tree RulesMatrix]=DecisionTree(DataSet,AttributName)
%输入为训练集,为离散后的数字,如记录1:1 1 3 2 1;
%前面为属性列,最后一列为类标
if nargin<1
error('请输入数据集');
else
if isstr(DataSet)
[DataSet AttributValue]=readdata2(DataSet);
else
AttributValue=[];
end
end
if nargin<2
AttributName=[];
end
Attributs=[1:size(DataSet,2)-1];
Tree=CreatTree(DataSet,Attributs);
disp([char() 'The Decision Tree:']);
showTree(Tree,0,0,1,AttributValue,AttributName);
Rules=getRule(Tree);
RulesMatrix=zeros(size(Rules,1),size(DataSet,2));
for i=1:size(Rules,1)
rule=cell2struct(Rules(i,1),{ 'str'});
rule=str2num([rule.str([1:(find(rule.str=='C')-1)]) rule.str((find(rule.str=='C')+1):length(rule.str))]);
for j=1:(length(rule)-1)/2
RulesMatrix(i,rule((j-1)*2+1))=rule(j*2);
end
RulesMatrix(i,size(DataSet,2))=rule(length(rule));
end
end
function Tree=CreatTree(DataSet,Attributs) %决策树程序 输入为:数据集,属性名列表
%disp(Attributs);
[S ValRecords]=ComputEntropy(DataSet,0);
if(S==0) %当样例全为一类时退出,返回叶子节点类标
for i=1:length(ValRecords)
if(length(ValRecords(i).matrix)==size(DataSet,1))
break;
end
end
Tree.Attribut=i;
Tree.Child=[];
return;
end
if(length(Attributs)==0) %当条件属性个数为0时返回占多数的类标
mostlabelnum=0;
mostlabel=0;
for i=1:length(ValRecords)
if(length(ValRecords(i).matrix)>mostlabelnum)
mostlabelnum=length(ValRecords(i).matrix);
mostlabel=i;
end
end
Tree.Attribut=mostlabel;
Tree.Child=[];
return;
end
for i=1:length(Attributs)
[Sa(i) ValRecord]=ComputEntropy(DataSet,i);
Gains(i)=S-Sa(i);
AtrributMatric(i).val=ValRecord;
end
[maxval maxindex]=max(Gains);
Tree.Attribut=Attributs(maxindex);
Attributs2=[Attributs(1:maxindex-1) Attributs(maxindex+1:length(Attributs))];
for j=1:length(AtrributMatric(maxindex).val)
DataSet2=[DataSet(AtrributMatric(maxindex).val(j).matrix',1:maxindex-1) DataSet(AtrributMatric(maxindex).val(j).matrix',maxindex+1:size(DataSet,2))];
if(size(DataSet2,1)==0)
mostlabelnum=0;
mostlabel=0;
for i=1:length(ValRecords)
if(length(ValRecords(i).matrix)>mostlabelnum)
mostlabelnum=length(ValRecords(i).matrix);
mostlabel=i;
end
end
Tree.Child(j).root.Attribut=mostlabel;
Tree.Child(j).root.Child=[];
else
Tree.Child(j).root=CreatTree(DataSet2,Attributs2);
end
end
end
function [Entropy RecordVal]=ComputEntropy(DataSet,attribut) %计算信息熵
if(attribut==0)
clnum=0;
for i=1:size(DataSet,1)
if(DataSet(i,size(DataSet,2))>clnum) %防止下标越界
classnum(DataSet(i,size(DataSet,2)))=0;
clnum=DataSet(i,size(DataSet,2));
RecordVal(DataSet(i,size(DataSet,2))).matrix=[];
end
classnum(DataSet(i,size(DataSet,2)))=classnum(DataSet(i,size(DataSet,2)))+1;
RecordVal(DataSet(i,size(DataSet,2))).matrix=[RecordVal(DataSet(i,size(DataSet,2))).matrix i];
end
Entropy=0;
for j=1:length(classnum)
P=classnum(j)/size(DataSet,1);
if(P~=0)
Entropy=Entropy+(-P)*log2(P);
end
end
else
valnum=0;
for i=1:size(DataSet,1)
if(DataSet(i,attribut)>valnum) %防止参数下标越界
clnum(DataSet(i,attribut))=0;
valnum=DataSet(i,attribut);
Valueexamnum(DataSet(i,attribut))=0;
RecordVal(DataSet(i,attribut)).matrix=[]; %将编号保留下来,以方便后面按值分割数据集
end
if(DataSet(i,size(DataSet,2))>clnum(DataSet(i,attribut))) %防止下标越界
Value(DataSet(i,attribut)).classnum(DataSet(i,size(DataSet,2)))=0;
clnum(DataSet(i,attribut))=DataSet(i,size(DataSet,2));
end
Value(DataSet(i,attribut)).classnum(DataSet(i,size(DataSet,2)))= Value(DataSet(i,attribut)).classnum(DataSet(i,size(DataSet,2)))+1;
Valueexamnum(DataSet(i,attribut))= Valueexamnum(DataSet(i,attribut))+1;
RecordVal(DataSet(i,attribut)).matrix=[RecordVal(DataSet(i,attribut)).matrix i];
end
Entropy=0;
for j=1:valnum
Entropys=0;
for k=1:length(Value(j).classnum)
P=Value(j).classnum(k)/Valueexamnum(j);
if(P~=0)
Entropys=Entropys+(-P)*log2(P);
end
end
Entropy=Entropy+(Valueexamnum(j)/size(DataSet,1))*Entropys;
end
end
end
function showTree(Tree,level,value,branch,AttributValue,AttributName)
blank=[];
for i=1:level-1
if(branch(i)==1)
blank=[blank ' |'];
else
blank=[blank ' '];
end
end
blank=[blank ' '];
if(level==0)
blank=[' (The Root):'];
else
if isempty(AttributValue)
blank=[blank '|_____' int2str(value) '______'];
else
blank=[blank '|_____' value '______'];
end
end
if(length(Tree.Child)~=0) %非叶子节点
if isempty(AttributName)
disp([blank 'Attribut ' int2str(Tree.Attribut)]);
else
disp([blank 'Attribut ' AttributName{ Tree.Attribut}]);
end
if isempty(AttributValue)
for j=1:length(Tree.Child)-1
showTree(Tree.Child(j).root,level+1,j,[branch 1],AttributValue,AttributName);
end
showTree(Tree.Child(length(Tree.Child)).root,level+1,length(Tree.Child),[branch(1:length(branch)-1) 0 1],AttributValue,AttributName);
else
for j=1:length(Tree.Child)-1
showTree(Tree.Child(j).root,level+1,AttributValue{ Tree.Attribut}{ j},[branch 1],AttributValue,AttributName);
end
showTree(Tree.Child(length(Tree.Child)).root,level+1,AttributValue{ Tree.Attribut}{ length(Tree.Child)},[branch(1:length(branch)-1) 0 1],AttributValue,AttributName);
end
else
if isempty(AttributValue)
disp([blank 'leaf ' int2str(Tree.Attribut)]);
else
disp([blank 'leaf ' AttributValue{ length(AttributValue)}{ Tree.Attribut}]);
end
end
end
function Rules=getRule(Tree)
if(length(Tree.Child)~=0)
Rules={ };
for i=1:length(Tree.Child)
content=getRule(Tree.Child(i).root);
%disp(content);
%disp([num2str(Tree.Attribut) ',' num2str(i) ',']);
for j=1:size(content,1)
rule=cell2struct(content(j,1),{ 'str'});
content(j,1)={ [num2str(Tree.Attribut) ',' num2str(i) ',' rule.str]};
end
Rules=[Rules;content];
end
else
Rules={ ['C' num2str(Tree.Attribut)]};
end
end
机器学习的特征重要性究竟是怎么算的
了解主流机器学习模型计算特征重要性的过程。常用算法包括xgboost、gbdt、randomforest、tree等,它们都能输出特征的重要性评分。本文将重点阐述xgboost和gbdt特征重要性计算方法。
xgboost计算特征重要性涉及到复杂的过程。在xgboost R API文档中能找到部分解释。在Python代码中,通过get_dump获取树规则,规则描述了特征在决策树中的使用情况。然而,原始的get_score方法输出的仅为统计值,包含权重、增益和覆盖度,未转换为百分比形式,这还不是真正的特征重要性得分。在xgboost的sklearn API中,feature_importance_方法对重要性统计量进行归一化处理,将之转换为百分比形式,计算分母为所有特征的重要性统计量之和。默认情况下,xgboost sklearn API计算重要性时使用importance_type="gain",而原始get_score方法使用importance_type="weight"。
对于gbdt,首先查找BaseGradientBoosting类,得到feature_importances_方法的源码。进一步追踪至tree模块,发现特征重要性来源于tree_.compute_feature_importances()方法。关于gbdt评估特征重要性的标准,存在疑问:它是依据分裂前后节点的impurity减少量进行评估。impurity的计算标准取决于节点的分裂标准,如MSE或MAE,具体在_criterion.pyx脚本中有所说明。gbdt中的树都是回归树,因此计算impurity的标准适用于该类问题。