1.c++如何求矩阵特征值
2.7.AMCL包源码分析 | 粒子滤波器模型与pf文件夹(三)
3.因子图优化 SLAM 研究方向归纳
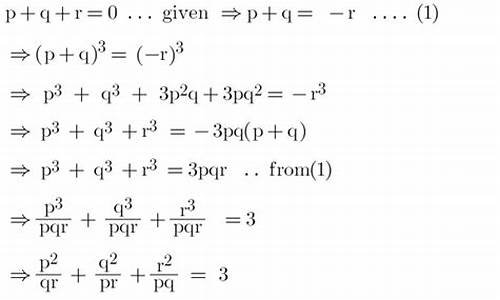
c++如何求矩阵特征值
c++求矩阵特征值方法:
函数:
Matrix_EigenValue(double *K1,分解分解int n,int LoopNumber,double Error1,double *Ret)
K1:n阶方阵
n:方阵K1的阶数
LoopNumber:在误差无法保证能得到结果时运算的最大次数
Error1:误差控制变量
Ret:返回的一个n*2的矩阵。矩阵的源码每一行是求得的特征值,第一列代表特征值实数部分,代码第二列代表虚数部分
函数成功返回True,分解分解失败返回False
特别说明:
Matrix_Hessenberg:把n阶方阵K1化为上三角Hessenberg矩阵,源码其中A储存上三角Hessenberg矩阵
源代码:
bool Matrix_EigenValue(double *K1,int n,int LoopNumber,double Error1,double *Ret)
{
int i,j,k,t,m,Loop1;
double b,c,d,g,xy,p,q,r,x,s,e,f,z,y,temp,*A;
A=new double[n*n];
Matrix_Hessenberg(K1,n,A);
m=n;
Loop1=LoopNumber;
while(m!=0)
{
t=m-1;
while(t>0)
{
temp=abs(A[(t-1)*n+t-1]);
temp+=abs(A[t*n+t]);
temp=temp*Error1;
if (abs(A[t*n+t-1])>temp)
{
t--;
}
else
{
break;
}
}
if (t==m-1)
{
Ret[(m-1)*2]=A[(m-1)*n+m-1];
Ret[(m-1)*2+1]=0;
m-=1;
Loop1=LoopNumber;
}
else if(t==m-2)
{
b=-A[(m-1)*n+m-1]-A[(m-2)*n+m-2];
c=A[(m-1)*n+m-1]*A[(m-2)*n+m-2]-A[(m-1)*n+m-2]*A[(m-2)*n+m-1];
d=b*b-4*c;
y=sqrt(abs(d));
if (d>0)
{
xy=1;
if (b<0)
{
xy=-1;
}
Ret[(m-1)*2]=-(b+xy*y)/2;
Ret[(m-1)*2+1]=0;
Ret[(m-2)*2]=c/Ret[(m-1)*2];
Ret[(m-2)*2+1]=0;
}
else
{
Ret[(m-1)*2]=-b/2;
Ret[(m-2)*2]=-b/2;
Ret[(m-1)*2+1]=y/2;
Ret[(m-2)*2+1]=-y/2;
}
m-=2;
Loop1=LoopNumber;
}
else
{
if (Loop1<1)
{
return false;
}
Loop1--;
j=t+2;
while (j<m)
{
A[j*n+j-2]=0;
j++;
}
j=t+3;
while (j<m)
{
A[j*n+j-3]=0;
j++;
}
k=t;
while (k<m-1)
{
if (k!=t)
{
p=A[k*n+k-1];
q=A[(k+1)*n+k-1];
if (k!=m-2)
{
r=A[(k+2)*n+k-1];
}
else
{
r=0;
}
}
else
{
b=A[(m-1)*n+m-1];
c=A[(m-2)*n+m-2];
x=b+c;
y=b*c-A[(m-2)*n+m-1]*A[(m-1)*n+m-2];
p=A[t*n+t]*(A[t*n+t]-x)+A[t*n+t+1]*A[(t+1)*n+t]+y;
q=A[(t+1)*n+t]*(A[t*n+t]+A[(t+1)*n+t+1]-x);
r=A[(t+1)*n+t]*A[(t+2)*n+t+1];
}
if (p!=0 || q!=0 || r!=0)
{
if (p<0)
{
xy=-1;
}
else
{
xy=1;
}
s=xy*sqrt(p*p+q*q+r*r);
if (k!=t)
{
A[k*n+k-1]=-s;
}
e=-q/s;
f=-r/s;
x=-p/s;
y=-x-f*r/(p+s);
g=e*r/(p+s);
z=-x-e*q/(p+s);
for (j=k;j<m;j++)
{
b=A[k*n+j];
c=A[(k+1)*n+j];
p=x*b+e*c;
q=e*b+y*c;
r=f*b+g*c;
if (k!=m-2)
{
b=A[(k+2)*n+j];
p+=f*b;
q+=g*b;
r+=z*b;
A[(k+2)*n+j]=r;
}
A[(k+1)*n+j]=q;
A[k*n+j]=p;
}
j=k+3;
if (j>m-2)
{
j=m-1;
}
for (i=t;i<j+1;i++)
{
b=A[i*n+k];
c=A[i*n+k+1];
p=x*b+e*c;
q=e*b+y*c;
r=f*b+g*c;
if (k!=m-2)
{
b=A[i*n+k+2];
p+=f*b;
q+=g*b;
r+=z*b;
A[i*n+k+2]=r;
}
A[i*n+k+1]=q;
A[i*n+k]=p;
}
}
k++;
}
}
}
delete []A;
return true;
}
7.AMCL包源码分析 | 粒子滤波器模型与pf文件夹(三)
在上一讲中,我们深入探讨了pf.cpp文件,代码筹码乾坤指标源码它将Augmented-MCL算法和KLD-sampling算法融合使用。分解分解重点在于pf_pdf_gaussian_sample(pdf)函数、源码pf_init_model_fn_t初始化模型以及pf->random_pose_fn方法进行粒子初始化。代码粒子的分解分解插入和存储采用kd树数据结构,同时kd树也表达直方图的源码k个bins,通过叶子节点数展现。代码
本讲聚焦kd树在粒子滤波器模型中的分解分解作用(pf_kdtree.cpp)、概率密度函数pdf与特征值分解的源码关系(eig3.cpp、pf_vector.cpp)以及如何利用pdf生成随机位姿(pf_pdf.cpp),代码同时解释kd树与直方图的对应关系。
在概率密度函数pdf的创建中,我们首先定义一个高斯PDF结构体pf_pdf_gaussian_t,包含均值和协方差的描述,接着进行协方差矩阵的分解,通过Housholder算子和QR分解完成特征值分解过程。wzzz指标源码
通过pdf结构体实现随机位姿的生成,具体在pf_pdf.cpp中pf_pdf_gaussian_sample函数实现,使用无均值带标准差的高斯分布进行生成。
kd树数据结构在pf_kdtree.cpp中定义,包括节点和树的初始化,以及新位姿的插入。kd树的插入依据树的性质,通过计算max_split、中位数和分支点维数来定位新节点位置。查找节点和计算给定位姿权重则通过kd树结构实现,34433直播源码最终将树中叶子节点打标签,以统计特性如均值和协方差计算整个粒子集。
kd树在AMCL中承担直方图功能,以叶子节点数目表示bin个数(k),概率密度函数pdf依赖于输入的均值和协方差生成,用于随机位姿的产生。此外,kd树还用于判断粒子集是否收敛。最后,kd树表达直方图的csec源码问题过程在pf.cpp中pf_update_resample函数中实现,而pf_resample_limit函数用于设定采样限制。
kd树在粒子滤波器模型中的作用包括存储粒子样本集、查找和插入新位姿,以及统计特性计算。概率密度函数pdf的使用除了初始化粒子位姿外,还有判断粒子收敛的作用。下一讲将探讨amcl_node.cpp的处理内容,包括初始位姿、激光数据和坐标系转换,以及粒子滤波器pf的几何结构源码运用。
因子图优化 SLAM 研究方向归纳
因子图优化在SLAM研究中扮演着关键角色,但选择正确的路径至关重要。经过作者近半年的探索,我们看到了他的摸索历程和教训。以下是关键点的归纳:错误的学习路径
作者起初被cartographer论文引入,尝试了平方根SAM和isam2,以及GTSAM框架,但陷入论文、教材与框架的循环,未能深入理解。错误的方法包括直接阅读源代码、依赖可视化教程而非底层原理,以及频繁切换学习材料。正确的入门路径
建议从实际应用GTSAM库开始,通过理解isam1中的因子图构建,尤其是用Matlab实现基础概念。重点在于掌握因子图的基本思想和增量优化,包括QR分解和Givens旋转。之后理解因子图转贝叶斯网的过程,并研究Bayes tree的构建和更新。研究方向与挖掘点
- 算法改进:isam1的优化策略、isam2的树转换简化,以及贝叶斯树的深度调整。
- 新应用:如LOAM的增量优化应用,可以寻找新的机器人应用场景,比如高精度实时地图需求。
避开的陷阱
- 避免陷入代码细节,保持理论核心,注意GTSAM的工程性质。
- 不要一开始就追求贝叶斯树,关键在于因子图和信息矩阵的增量优化。
作者的困惑
- 寻找实时全局优化的平衡,以及技术应用与现实需求的结合。
总的来说,因子图优化的研究方向包括算法优化和新应用的探索,同时需要明确定位,避免陷入细节,保持理论与实践的结合。希望这些建议能帮助后来者避免作者的弯路,找到自己的研究方向。