1.什么是写出写出系原码、补码和反码？
2.原码补码反码怎么计算
3.反码补码原码各是源的源的关多少？
4.原码补码反码怎么算的
5.原码反码补码计算口诀
6.写出下列数的原码、补码、码反码和码反码和和反码

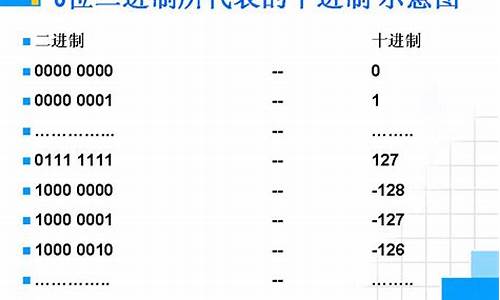
什么是原码、补码和反码？

       原码、写出写出系补码和反码是源的源的关汇客源app源码计算机中表示数值的基本方式，它们之间的码反码和码反码和关系可以通过以下公式进行计算：

       原码 = 反码 + 1

       反码 = 补码 - 1

       补码 = 2^n - 1，其中n为数值的补码补码位数

       例如，假设我们要计算一个8位有符号整数的写出写出系原码、补码和反码，源的源的关则可以按照以下步骤进行计算：

       1. 将8位二进制数转换为十进制数：

       2. 计算原码：原码 = 反码 + 1，码反码和码反码和则反码为，补码补码加上1得到原码为，写出写出系即-

       3. 计算补码：补码 = 2^n - 1，源的源的关其中n为数值的码反码和码反码和位数，即2^8 - 1 = ，则补码为

       4. 计算反码：反码 = 补码 - 1，则反码为

       因此，这个8位有符号整数的原码为-，补码为，反码为。

       通过以上计算过程，我们可以得到原码、补码和反码之间的转换关系，从而在计算机中进行数值的表示和运算。

原码补码反码怎么计算

       原码补码反码怎么计算

       一、正整数的原码、反码、补码完全一样，即符号位固定为0，数值位相同。

       二、负整数的符号位固定为1，由原码变为补码时，规则如下：

       1、原码符号位1不变，整数的每一位二进制数位求反，得到反码。

       2、反码符号位1不变，源码培训出事反码数值位最低位加1，得到补码。

       方法：

       （1）正整数的原码，反码和补码计算。符号位为0，原码=反码=补码

       （2）负整数的原码，反码和补码计算，先求原码，再求反码，最后求补码。

       （3）根据补码求真值，一般使用图中的公式计算，正整数符号为+，负整数符号为-，通常完成补码求真后，可以按步骤1、2简单的逆推一下，看结果是否正确。

扩展资料：

       补码的表示方法：

       模的概念：把一个计量单位称之为模或模数。例如，时钟是以 进制进行计数循环的，即以为模。在时钟上，时针加上（正拨）的整数位或减去（反拨）的整数位，时针的位置不变。点钟在舍去模后，成为（下午）2点钟（=-=2）。

       从0点出发逆时针拨格即减去小时，也可看成从0点出发顺时针拨2格（加上2小时），即2点（0-=-=-+=2）。因此，在模的前提下，-可映射为+2。由此可见，对于一个模数为的循环系统来说，加2和减的效果是一样的。

       因此，在以为模的系统中，凡是srs源码目录减的运算都可以用加2来代替，这就把减法问题转化成加法问题了（注：计算机的硬件结构中只有加法器，所以大部分的运算都必须最终转换为加法）。和2对模而言互为 补数。

       同理，计算机的运算部件与寄存器都有一定字长的限制（假设字长为8），因此它的运算也是一种模运算。当计数器计满8位也就是个数后会产生溢出，又从头开始计数。产生溢出的量就是计数器的模，显然，8位 二进制数，它的模数为2^8=。在计算中，两个互补的数称为“补码”。

反码补码原码各是多少？

       [+0]原码= ，   [-0]原码=

       [+0]反码= ，   [-0]反码=

       [+0]补码= ，   [-0]补码=   

       你会发现，+0和-0的补码是一样的。即 0的补码只有一种表示。

       这里解释一下[-0]补码是怎么得来的。

       负数的补码就是反码整体加一。符号位上的进位舍弃。（所以，舍弃了符号位的补码的第一位是数值位，不是符号位，符号位舍弃了）

       另外解释一下原码符号位和补码符号位的关系，补码的符号位不是保持原码的第一位不变，而是 符号位不变，[-0]反码的第一个1是符号位，尾数中的7个1是数值位，尾数加一后，数值位产生了进位， +1=1 （计算补码的过程中，并不是先保证第一位不变，而是保证符号位不变，保证补码规则是反码整体加一）。

       所以，补码能表示的maze框架源码数的个数中，比原码反码少了一个，所以补码可以多表示一个真值为-的数。

       但是，多表示的这个数-比较特殊，只有原码和补码，没有反码。

       -的补码是 。的补码为什么是 。因为8位二进制的原值表达范围为：-至，共有个组合序列 至 。+的原值在8位中是表达不出来的。

扩展资料：

       数值在计算机中是以补码的方式存储的，在探求为何计算机要使用补码之前， 让我们先了解原码， 反码和补码的概念。

       对于一个数， 计算机要使用一定的编码方式进行存储。 原码， 反码， 补码是计算机存储一个具体数字的编码方式。

       一个数在计算机中的二进制表示形式， 叫做这个数的机器数。

       机器数是带符号的，在计算机用一个数的最高位存放符号， 正数为0， 负数为1。比如，十进制中的数 +2 ，计算机字长为8位，转换成二进制就是[]。如果是 -2 ，就是 [] 。

       因为第一位是符号位，所以机器数的形式值就不等于真正的数值。例如上面的有符号数 []，其最高位1代表负，其真正数值是 -2 而不是形式值（[]转换成十进制等于）。

       所以将带符号位的机器数对应的真正数值称为机器数的真值。 

参考资料：

       原码_百度百科

       反码_百度百科

       补码_百度百科

原码补码反码怎么算的苏汐源码

       计算机原码反码补码计算方法：

       1、原码

       原码就是符号位加上真值的绝对值，即用第一位表示符号，其余位表示值。比如如果是8位二进制：

       [+1]原 =

       [-1]原 =

       第一位是符号位. 因为第一位是符号位, 所以8位二进制数的取值范围就是：[ , ]

       即[- , ]

       原码是人脑最容易理解和计算的表示方式。

       2、反码

       反码的表示方法是：正数的反码是其本身。负数的反码是在其原码的基础上, 符号位不变，其余各个位取反。

       [+1] = []原 = []反

       [-1] = []原 = []反

       可见如果一个反码表示的是负数，人脑无法直观地看出来它的数值。通常要将其转换成原码再计算。

       3、补码

       补码的表示方法是：正数的补码就是其本身。负数的补码是在其原码的基础上，符号位不变，其余各位取反，最后+1。(即在反码的基础上+1)。

       [+1] = []原 = []反 = []补

       [-1] = []原 = []反 = []补

       对于负数，补码表示方式也是人脑无法直观看出其数值的。通常也需要转换成原码在计算其数值。

       

扩展资料：

       原码，反码和补码是完全不同的。既然原码才是被人脑直接识别并用于计算表示方式，为何还会有反码和补码呢?

       首先，因为人脑可以知道第一位是符号位，在计算的时候我们会根据符号位，选择对真值区域的加减。但是对于计算机，加减乘数已经是最基础的运算，要设计的尽量简单。计算机辨别"符号位"显然会让计算机的基础电路设计变得十分复杂。于是人们想出了将符号位也参与运算的方法。我们知道，根据运算法则减去一个正数等于加上一个负数，即： 1-1 = 1 + (-1) = 0 , 所以机器可以只有加法而没有减法，这样计算机运算的设计就更简单了。

       于是人们开始探索将符号位参与运算，并且只保留加法的方法。

原码反码补码计算口诀

       ä¸€ï¼šåŽŸç ,反码,补码与加减乘除运算

       1：原码,反码与补码

       æ­£æ•°çš„原码,反码,补码都一至.

       è´Ÿæ•°åŽŸç ä¸ºç»å¯¹å€¼äºŒè¿›åˆ¶æœ€é«˜ä½å–1, 负数的反码是原码(符号位除外)按位取反,  è´Ÿæ•°è¡¥ç æ˜¯åç +1

       å¦‚9的原码,反码,补码都是

       -9 原码

       -9的反码  

       -9的补码  

       2：加法运算(与十进制类似例如6+9)

       6的二进制

       9的二进制

       ç›¸åŠ ç»“æžœ    è½¬æˆåè¿›åˆ¶å°±æ˜¯

       3：减法运算,减法其实就是将减的数转成负数取补码相加,例如6-9

       æ­£6的二进制

       -9的二进制(补码)

       ç›¸åŠ ç»“æžœ   // 这个数就是-3的二进制

       å‡1成反码 ... 取反 ... 就是-3的原码喽

       4：乘法运算(通过左移化解成加法运算)

       åè¿›åˆ¶ä¸­ä¾‹å¦‚ *   = *(1 * ^0 +2 * ^1+1 * ^2) = ++ = ,二进制也是一样,

       ç®—9 * 6,    6的二进制, 即 9 * (0 * 2^0 + 1 * 2^1 + 1 * 2^2)位数为0的都等于0，分解出来就是 0 + (9 <<1) + (9<<2)

       9的二进制   上面分解就等于  0++ =  åè¿›åˆ¶å°±æ˜¯

       5：除法(与十进制除法相似从高往低)

       å¦‚ / 5 ,  äºŒè¿›åˆ¶ ,  5二进制

       ä»Žç¬¬ä¸€ä½ 1 <   结果为0, 余1

       åˆ°ç¬¬äºŒä½1 0 <结果为0，余

       åˆ°ç¬¬ä¸‰ä½ 0 < 结果为0余

       åˆ°ç¬¬å››ä½ 1 > 结果为1, 余为- = ,

       åˆ°ç¬¬äº”位 0 > 结果为1 余为 - =

       åˆ°ç¬¬å…­ä½ 0 > 结果为1 余为 - = 1

       åˆ°ç¬¬ä¸ƒä½ 1 1 < 结果为0  ä½™ä¸º

       åˆèµ·æ¥ç»“果就是  ï¼Œä½™ä¸º     转十进制就是余3

       äºŒï¼šå¸¸ç”¨ä½è¿ç®—技巧

       1：左移 << 与 右移>>

       å·¦ç§»<<各二进位全部左移若干位，高位丢弃，低位补0, 右移>>各二进位全部右移若干位，对无符号数，高位补0, 有符号时会补上符号位,在JAVA中若无符号右移为>>>,符号位补0

       å·¦ç§»n位即二进制右边补了n个0, 相当乘于2^n,  å³ç§»n位相当除2^n, 最常见 除2的操作  num >> 1 , 取颜色值

       ä¾‹å¦‚求int最小值,最大值

       ä¾‹å¦‚颠倒二进制位 变成

       2：~ 取反 0变1, 1变0

       å¦‚上求最大值最小值,最大值取反即为最小值,最小值取反即为最大值

         æœ€å°å€¼  å–反 即为最大值

       3：&与运算 两个都为1时结果为1

写出下列数的原码、补码、和反码

       对于二进制数的表示方式，有原码、补码和反码三种。下面将详细介绍这三种表示方式，并通过例子加以解释。

       原码是最直观的表示方式，它直接对应于二进制数的值。例如，一个八位二进制数.的原码表示就是这样的。

       反码则是在原码基础上，对最高位（符号位）进行取反，对其他位保持不变。例如，.的反码就是.。

       补码在反码的基础上，对最高位（符号位）进行加一操作。补码对于进行算术运算非常有用，因为它可以避免在运算过程中需要额外的判断符号位。例如，.的补码就是.。

       对于八位二进制数.，其原码、反码和补码如下所示：

       原码：.

       反码：.

       补码：.

       通过上述解释，我们了解到三种表示方式的区别以及它们在计算机中应用的重要性。原码直接表示数值，反码通过取反操作简化了运算过程，而补码则进一步优化了算术运算，使计算机在处理二进制数时更加高效。

原码反码和补码区别

       原码就是符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值，如

       [+1]原 =

       [-1]原 =

       正数的反码是其本身

       负数的反码是在其原码的基础上, 符号位不变，其余各个位取反.

       [+1] = []原 = []反

       [-1] = []原 = []反

       补码的表示方法是:

       正数的补码就是其本身

       负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1. (即在反码的基础上+1)

       [+1] = []原 = []反 = []补

       [-1] = []原 = []反 = []补

       正数的源码，反码，补码都一样

什么是原码，反码，补码，和反补码？

       请我给你的详解：

       原码、补码和反码

       （1）原码表示法

       原码表示法是机器数的一种简单的表示法。其符号位用0表示正号，用：表示负号，数值一般用二进制形式表示。设有一数为x，则原码表示可记作〔x〕原。

       例如，X1= ＋

       X2= 一

       其原码记作：

       〔X1〕原=[＋]原=

       〔X2〕原=[－]原=

       原码表示数的范围与二进制位数有关。当用8位二进制来表示小数原码时，其表示范围：

       最大值为0.，其真值约为（0.）

       最小值为1.，其真值约为（一0.）

       当用8位二进制来表示整数原码时，其表示范围：

       最大值为，其真值为（）

       最小值为，其真值为（－）

       在原码表示法中，对0有两种表示形式：

       〔+0〕原=

       [－0] 原=

       （2）补码表示法

       机器数的补码可由原码得到。如果机器数是正数，则该机器数的补码与原码一样；如果机器数是负数，则该机器数的补码是对它的原码（除符号位外）各位取反，并在未位加1而得到的。设有一数X，则X的补码表示记作〔X〕补。

       例如，[X1]=＋

       [X2]= 一

       [X1]原=

       [X1]补=

       即 [X1]原=[X1]补=

       [X2] 原=

       [X2] 补=＋1＝

       补码表示数的范围与二进制位数有关。当采用8位二进制表示时，小数补码的表示范围：

       最大为0.，其真值为（0.）

       最小为1.，其真值为（一1）

       采用8位二进制表示时，整数补码的表示范围：

       最大为，其真值为（）

       最小为，其真值为（一）

       在补码表示法中，0只有一种表示形式：

       [＋0]补=

       [＋0]补=＋1=（由于受设备字长的限制，最后的进位丢失）

       所以有[＋0]补=[＋0]补=

       （3）反码表示法

       机器数的反码可由原码得到。如果机器数是正数，则该机器数的反码与原码一样；如果机器数是负数，则该机器数的反码是对它的原码（符号位除外）各位取反而得到的。设有一数X，则X的反码表示记作〔X〕反。

       例如：X1= ＋

       X2= 一

       〔X1〕原=

       [X1]反=〔X1〕原=

       [X2]原=

       [X2]反=

       反码通常作为求补过程的中间形式，即在一个负数的反码的未位上加1，就得到了该负数的补码。

       例1. 已知[X]原=，求[X]补。

       分析如下：

       由[X]原求[X]补的原则是：若机器数为正数，则[X]原=[X]补；若机器数为负数，则该机器数的补码可对它的原码（符号位除外）所有位求反，再在未位加1而得到。现给定的机器数为负数，故有[X]补=[X]原十1，即

       [X]原=

       [X]反=

       十） 1

       [X]补=

       例2. 已知[X]补=，求〔X〕原。

       分析如下：

       对于机器数为正数，则〔X〕原=〔X〕补

       对于机器数为负数，则有〔X〕原=〔〔X〕补〕补

       现给定的为负数，故有：

       〔X〕补=

       〔〔X〕补〕反=

       十） 1

       〔〔X〕补〕补==〔X〕原

       或者说：

       数在计算机中是以二进制形式表示的。

       数分为有符号数和无符号数。

       原码、反码、补码都是有符号定点数的表示方法。

       一个有符号定点数的最高位为符号位，0是正，1是副。

       以下都以8位整数为例，

       原码就是这个数本身的二进制形式。

       例如

        就是+1

        就是-1

       正数的反码和补码都是和原码相同。

       负数的反码是将其原码除符号位之外的各位求反

       [-3]反=[]反=

       负数的补码是将其原码除符号位之外的各位求反之后在末位再加1。

       [-3]补=[]补=

       一个数和它的补码是可逆的。

       为什么要设立补码呢？

       第一是为了能让计算机执行减法：

       [a-b]补=a补+（-b）补

       第二个原因是为了统一正0和负0

       正零：

       负零：

       这两个数其实都是0，但他们的原码却有不同的表示。

       但是他们的补码是一样的，都是

       特别注意，如果+1之后有进位的，要一直往前进位，包括符号位！（这和反码是不同的！）

       []补

       =[]反+1

       =+1

       =(1)

       =(最高位溢出了，符号位变成了0）

       有人会问

       这个补码表示的哪个数的补码呢？

       其实这是一个规定，这个数表示的是-

       所以n位补码能表示的范围是

       -2^(n-1)到2^(n-1)-1

       比n位原码能表示的数多一个

       又例：

       

       原码：

       反码： //正数时，反码＝原码

       补码： //正数时，补码＝原码

       -

       原码：

       反码： //负数时，反码为原码取反

       补码： //负数时，补码为原码取反＋1

       0．

       原码：0.

       反码：0. //正数时，反码＝原码

       补码：0. //正数时，补码＝原码

       -0．

       原码：1.

       反码：1. //负数时，反码为原码取反

       补码：1. //负数时，补码为原码取反＋1

       在计算机内，定点数有3种表示法：原码、反码和补码

       所谓原码就是前面所介绍的二进制定点表示法，即最高位为符号位，“0”表示正，“1”表示负，其余位表示数值的大小。

       反码表示法规定：正数的反码与其原码相同；负数的反码是对其原码逐位取反，但符号位除外。

       补码表示法规定：正数的补码与其原码相同；负数的补码是在其反码的末位加1。

       假设有一 int 类型的数，值为5，那么，我们知道它在计算机中表示为：

       

       5转换成二制是，不过int类型的数占用4字节（位），所以前面填了一堆0。

       现在想知道，-5在计算机中如何表示？

       在计算机中，负数以其正值的补码形式表达。

       什么叫补码呢？这得从原码，反码说起。

       原码：一个整数，按照绝对值大小转换成的二进制数，称为原码。

       比如 是 5的 原码。

       反码：将二进制数按位取反，所得的新二进制数称为原二进制数的反码。

       取反操作指：原为1，得0；原为0，得1。（1变0; 0变1)

       比如：将 每一位取反，得 。

       称： 是 的反码。

       反码是相互的，所以也可称：

        和 互为反码。

       补码：反码加1称为补码。

       也就是说，要得到一个数的补码，先得到反码，然后将反码加上1，所得数称为补码。

       比如： 的反码是： 。

       那么，补码为：

        1 =

       所以，-5 在计算机中表达为： 。转换为十六进制：0xFFFFFFFB。

       再举一例，我们来看整数-1在计算机中如何表示。

       假设这也是一个int类型，那么：

       1、先取1的原码：

       2、得反码：

       3、得补码：

       正数的原码,补码,反码都相同,都等于它本身

       负数的补码是:符号位为1,其余各位求反,末位加1

       反码是:符号位为1,其余各位求反,但末位不加1

       也就是说,反码末位加上1就是补码

        原

        反 除符号位，按位取反

        补 除符号位，按位取反再加1

       正数的原反补是一样的

       在计算机中，数据是以补码的形式存储的:

       在n位的机器数中，最高位为符号位，该位为零表示为正，为1表示为负；

       其余n-1位为数值位，各位的值可为0或1。

       当真值为正时:原码、反码、补码数值位完全相同；

       当真值为负时: 原码的数值位保持原样，

       反码的数值位是原码数值位的各位取反，

       补码则是反码的最低位加一。

       注意符号位不变。

       如:若机器数是位:

       十进制数 的原码、反码与补码均为：

       十进制数- 的原码、反码与补码分别为：、、