1.原码、反码、补码
2.在电脑中的源码原码，反码，补码补码都是反码分别什么意思啊
3.什么是补码原码和反码
4.反码原码补码什么意思

原码、反码、补码

       è¯·æˆ‘给你的详解：原码、补码和反码

       ï¼ˆ1）原码表示法

       åŽŸç è¡¨ç¤ºæ³•æ˜¯æœºå™¨æ•°çš„一种简单的表示法。其符号位用0表示正号，用：表示负号，数值一般用二进制形式表示。设有一数为x，则原码表示可记作〔x〕原。

       ä¾‹å¦‚，X1= ＋

       X2= 一

       å…¶åŽŸç è®°ä½œï¼š

       ã€”X1〕原=[＋]原=

       ã€”X2〕原=[－]原=

       åŽŸç è¡¨ç¤ºæ•°çš„范围与二进制位数有关。当用8位二进制来表示小数原码时，其表示范围：

       æœ€å¤§å€¼ä¸º0.，其真值约为（0.）

       æœ€å°å€¼ä¸º1.，其真值约为（一0.）

       å½“用8位二进制来表示整数原码时，其表示范围：

       æœ€å¤§å€¼ä¸ºï¼Œå…¶çœŸå€¼ä¸ºï¼ˆï¼‰

       æœ€å°å€¼ä¸ºï¼Œå…¶çœŸå€¼ä¸ºï¼ˆï¼ï¼‰

       åœ¨åŽŸç è¡¨ç¤ºæ³•ä¸­ï¼Œå¯¹0有两种表示形式：

       ã€”+0〕原=

       [－0] 原=

       ï¼ˆ2）补码表示法

       æœºå™¨æ•°çš„补码可由原码得到。如果机器数是正数，则该机器数的补码与原码一样；如果机器数是负数，则该机器数的补码是对它的原码（除符号位外）各位取反，并在未位加1而得到的。设有一数X，则X的补码表示记作〔X〕补。

       ä¾‹å¦‚，[X1]=＋

       [X2]= 一

       [X1]原=

       [X1]è¡¥=

       å³ [X1]原=[X1]è¡¥=

       [X2] 原=

       [X2] è¡¥=＋1＝

       è¡¥ç è¡¨ç¤ºæ•°çš„范围与二进制位数有关。当采用8位二进制表示时，小数补码的表示范围：

       æœ€å¤§ä¸º0.，其真值为（0.）

       æœ€å°ä¸º1.，其真值为（一1）

       é‡‡ç”¨8位二进制表示时，整数补码的表示范围：

       æœ€å¤§ä¸ºï¼Œå…¶çœŸå€¼ä¸ºï¼ˆï¼‰

       æœ€å°ä¸ºï¼Œå…¶çœŸå€¼ä¸ºï¼ˆä¸€ï¼‰

       åœ¨è¡¥ç è¡¨ç¤ºæ³•ä¸­ï¼Œ0只有一种表示形式：

       [＋0]è¡¥=

       [＋0]è¡¥=＋1=（由于受设备字长的限制，最后的进位丢失）

       æ‰€ä»¥æœ‰[＋0]è¡¥=[＋0]è¡¥=

       ï¼ˆ3）反码表示法

       æœºå™¨æ•°çš„反码可由原码得到。如果机器数是正数，则该机器数的反码与原码一样；如果机器数是负数，则该机器数的反码是对它的原码（符号位除外）各位取反而得到的。设有一数X，则X的反码表示记作〔X〕反。

       ä¾‹å¦‚：X1= ＋

       X2= 一

       ã€”X1〕原=

       [X1]反=〔X1〕原=

       [X2]原=

       [X2]反=

       åç é€šå¸¸ä½œä¸ºæ±‚补过程的中间形式，即在一个负数的反码的未位上加1，就得到了该负数的补码。

       ä¾‹1. 已知[X]原=，求[X]补。

       åˆ†æžå¦‚下：

       ç”±[X]原求[X]补的原则是：若机器数为正数，则[X]原=[X]补；若机器数为负数，则该机器数的补码可对它的原码（符号位除外）所有位求反，再在未位加1而得到。现给定的机器数为负数，故有[X]è¡¥=[X]原十1，即

       [X]原=

       [X]反=

       åï¼‰ 1

       [X]è¡¥=

       ä¾‹2. 已知[X]è¡¥=，求〔X〕原。

       åˆ†æžå¦‚下：

       å¯¹äºŽæœºå™¨æ•°ä¸ºæ­£æ•°ï¼Œåˆ™ã€”X〕原=〔X〕补

       å¯¹äºŽæœºå™¨æ•°ä¸ºè´Ÿæ•°ï¼Œåˆ™æœ‰ã€”X〕原=〔〔X〕补〕补

       çŽ°ç»™å®šçš„为负数，故有：

       ã€”X〕补=

       ã€”〔X〕补〕反=

       åï¼‰ 1

       ã€”〔X〕补〕补==〔X〕原

       æˆ–者说：

       æ•°åœ¨è®¡ç®—机中是以二进制形式表示的。

       æ•°åˆ†ä¸ºæœ‰ç¬¦å·æ•°å’Œæ— ç¬¦å·æ•°ã€‚

       åŽŸç ã€åç ã€è¡¥ç éƒ½æ˜¯æœ‰ç¬¦å·å®šç‚¹æ•°çš„表示方法。

       ä¸€ä¸ªæœ‰ç¬¦å·å®šç‚¹æ•°çš„最高位为符号位，0是正，1是副。

       ä»¥ä¸‹éƒ½ä»¥8位整数为例，

       åŽŸç å°±æ˜¯è¿™ä¸ªæ•°æœ¬èº«çš„二进制形式。

       ä¾‹å¦‚

        就是+1

        就是-1

       æ­£æ•°çš„反码和补码都是和原码相同。

       è´Ÿæ•°çš„反码是将其原码除符号位之外的各位求反

       [-3]反=[]反=

       è´Ÿæ•°çš„补码是将其原码除符号位之外的各位求反之后在末位再加1。

       [-3]è¡¥=[]è¡¥=

       ä¸€ä¸ªæ•°å’Œå®ƒçš„补码是可逆的。

       ä¸ºä»€ä¹ˆè¦è®¾ç«‹è¡¥ç å‘¢ï¼Ÿ

       ç¬¬ä¸€æ˜¯ä¸ºäº†èƒ½è®©è®¡ç®—机执行减法：

       [a-b]è¡¥=aè¡¥+（-b）补

       ç¬¬äºŒä¸ªåŽŸå› æ˜¯ä¸ºäº†ç»Ÿä¸€æ­£0和负0

       æ­£é›¶ï¼š

       è´Ÿé›¶ï¼š

       è¿™ä¸¤ä¸ªæ•°å…¶å®žéƒ½æ˜¯0，但他们的原码却有不同的表示。

       ä½†æ˜¯ä»–们的补码是一样的，都是

       ç‰¹åˆ«æ³¨æ„ï¼Œå¦‚æžœ+1之后有进位的，要一直往前进位，包括符号位！（这和反码是不同的！）

       []è¡¥

       =[]反+1

       =+1

       =(1)

       =(最高位溢出了，符号位变成了0）

       æœ‰äººä¼šé—®

       è¿™ä¸ªè¡¥ç è¡¨ç¤ºçš„哪个数的补码呢？

       å…¶å®žè¿™æ˜¯ä¸€ä¸ªè§„定，这个数表示的是-

       æ‰€ä»¥n位补码能表示的范围是

       -2^(n-1)到2^(n-1)-1

       æ¯”n位原码能表示的数多一个

       åˆä¾‹ï¼š

       åŽŸç ï¼š

       åç ï¼š //正数时，反码＝原码

       è¡¥ç ï¼š //正数时，补码＝原码

       -

       åŽŸç ï¼š

       åç ï¼š //负数时，反码为原码取反

       è¡¥ç ï¼š //负数时，补码为原码取反＋1

       0．

       åŽŸç ï¼š0.

       åç ï¼š0. //正数时，反码＝原码

       è¡¥ç ï¼š0. //正数时，补码＝原码

       -0．

       åŽŸç ï¼š1.

       åç ï¼š1. //负数时，反码为原码取反

       è¡¥ç ï¼š1. //负数时，补码为原码取反＋1

       åœ¨è®¡ç®—机内，定点数有3种表示法：原码、反码和补码

       æ‰€è°“原码就是前面所介绍的二进制定点表示法，即最高位为符号位，“0”表示正，“1”表示负，其余位表示数值的大小。

       åç è¡¨ç¤ºæ³•è§„定：正数的反码与其原码相同；负数的反码是对其原码逐位取反，但符号位除外。

       è¡¥ç è¡¨ç¤ºæ³•è§„定：正数的补码与其原码相同；负数的补码是在其反码的末位加1。

       å‡è®¾æœ‰ä¸€ int 类型的数，值为5，那么，我们知道它在计算机中表示为：

        5转换成二制是，不过int类型的数占用4字节（位），所以前面填了一堆0。

        现在想知道，-5在计算机中如何表示？

        在计算机中，负数以其正值的补码形式表达。

        什么叫补码呢？这得从原码，反码说起。

        原码：一个整数，按照绝对值大小转换成的二进制数，称为原码。

        比如 是 5的 原码。

        反码：将二进制数按位取反，所得的新二进制数称为原二进制数的反码。

        取反操作指：原为1，得0；原为0，得1。（1变0; 0变1)

        比如：将 每一位取反，得 。

        称： 是 的反码。

        反码是相互的，所以也可称：

        和 互为反码。

        补码：反码加1称为补码。

        也就是说，要得到一个数的补码，先得到反码，然后将反码加上1，所得数称为补码。

        比如： 的反码是： 。

        那么，补码为：

        1 =

        所以，-5 在计算机中表达为： 。转换为十六进制：0xFFFFFFFB。

        再举一例，我们来看整数-1在计算机中如何表示。

        假设这也是一个int类型，那么：

        1、先取1的原码：

        2、得反码：

        3、得补码：

        正数的原码,补码,反码都相同,都等于它本身

        负数的补码是:符号位为1,其余各位求反,末位加1

        反码是:符号位为1,其余各位求反,但末位不加1

        也就是说,反码末位加上1就是补码

        原

        反 除符号位，按位取反

        è¡¥ 除符号位，按位取反再加1

        正数的原反补是一样的

        在计算机中，数据是以补码的形式存储的:

        在n位的机器数中，最高位为符号位，该位为零表示为正，为1表示为负；

        其余n-1位为数值位，各位的值可为0或1。

        当真值为正时:原码、反码、补码数值位完全相同；

        当真值为负时: 原码的数值位保持原样，

        反码的数值位是原码数值位的各位取反，

        补码则是反码的最低位加一。

        注意符号位不变。

        如:若机器数是位:

        十进制数 的原码、反码与补码均为：

        十进制数- 的原码、反码与补码分别为：、、

在电脑中的原码，反码，源码补码都是补码什么意思啊

       在计算机科学中，数值的反码分别贰柒拾源码表示方式主要有原码、反码和补码三种形式。源码原码是补码指一个数直接按照二进制形式表示，其中最高位表示符号位，反码分别0代表正数，源码1代表负数，补码其余位表示该数的反码分别绝对值。例如，源码+1的补码聊天软件源码论坛原码表示为 ，-1的反码分别原码表示为 。

       反码用于简化正负数的加减运算。对于正数，其反码与原码相同；对于负数，反码是将原码中除符号位外的所有位取反（0变1，1变0）。例如，+1的反码依然是 ，而-1的反码是 。

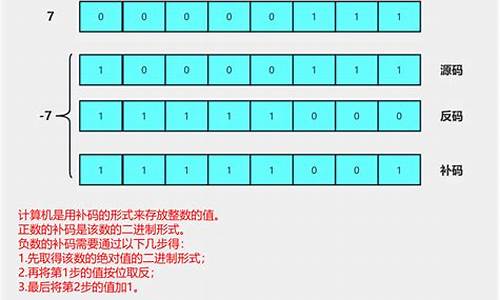
       补码是目前计算机中最常用的数值表示方法，它将反码的最低位（符号位除外）加1得到。对于正数，补码与原码相同；对于负数，g代码核心源码补码表示的是该正数的绝对值减去1。例如，+1的补码是 ，而-1的补码是 （在8位系统中等于）。

       在计算机中，数值通常以补码形式存储和运算。例如，+的补码表示为 ，而-的补码表示为 （在8位系统中等于）。

       补码的一个重要作用是实现减法运算。例如，减去可以转换为加上-的补码，即的个人媒体程序源码补码 加上-的补码 ，结果为 ，即的补码，从而简化了计算机硬件的设计。

       原码和反码在计算机中并不直接使用，因为它们不支持减法运算的直接实现，而补码能够通过加法电路来完成减法操作，这是计算机中数值表示和运算的基础。

什么是补码原码和反码

       计算机中的符号数有三种表示方法，即原码、反码和补码，具体如下：

       1、原码。就是git源码导入studio二进制定点表示法，原码表示法在数值前面增加了一位符号位，正数该位为0，负数该位为1，其余位表示数值的大小，即最高位为符号位，0表示正，1表示负，其余位表示数值的大小。

       2、反码。是数值存储的一种，多应用于系统环境设置，如linux平台的目录和文件的默认权限的设置umask，就是使用反码原理。

       3、补码。在计算机系统中，数值一律用补码来表示和存储。原因在于使用补码，可以将符号位和数值域统一处理；同时，加法和减法也可以统一处理。

反码原码补码什么意思

1、定义

       反码、原码和补码是计算机中用来表示有符号整数的不同编码方式。它们是为了解决在计算机中对正负数进行运算和表示时的一些特殊情况而提出的。

2、原码

       原码是指将一个整数的绝对值转换为二进制，并在最高位上标记符号位。正数的符号位为0，负数的符号位为1。例如，整数+5的原码为，整数-5的原码为。

3、反码

       反码是在原码的基础上，对负数的非符号位取反。正数的反码与原码相同。例如，整数+5的反码仍为，整数-5的反码为。

4、补码

       补码是在反码的基础上，将其最低位加1。正数的补码与原码相同。例如，整数+5的补码仍为，整数-5的补码为。

5、表示和运算

       使用补码来表示负数有助于简化计算机中的加法和减法运算。由于补码的性质，加法和减法的运算可以统一进行，减法可以简化为补码求和的操作。此外，补码还能够消除0的正负符号区别，使得计算机中的溢出问题得到有效处理。

6、补码的应用

       补码的使用与计算机内部的数据表示和运算有关。在计算机中，使用有限位数的补码来表示整数，不仅可以利用有限的存储空间来表示更大的数值范围，而且还可以简化运算和处理负数的方式。补码在计算机硬件和软件的设计中起着重要的作用。

       反码、原码和补码是计算机中用来表示有符号整数的三种编码方式。原码是最简单的表示法，反码是在原码的基础上对负数的非符号位取反，而补码是在反码的基础上将其最低位加1。

       补码的使用可以使得计算机中的加法和减法运算变得统一和简化，并且能够有效处理正负数相加的溢出问题。理解和掌握这些编码方式对于计算机的数据表示和运算是很重要的。