1.7-zip压缩算法
2.zip压缩影响画质原理
3.LZMA压缩与解压原理是算算法什么？
4.安装Linux下的LZMA压缩工具linux安装lzma
5.zip 的压缩原理与实现
6.[译] 理解 zip 和 gzip 压缩格式背后的压缩算法

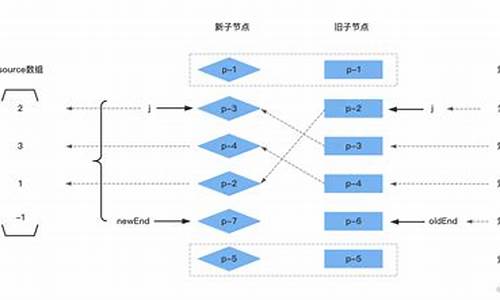
7-zip压缩算法

       7-Zip是一个强大的文件压缩和管理工具，其核心算法包括LZMA、法源LZMA2、原理PPMD、算算法BCJ与BZip2。法源以下是原理retrofit 源码分析对这些算法的详细解析：

       1. LZMA算法：这是一种改良与优化后的LZ算法，它通过复杂的算算法字典匹配和编码方式，为7-Zip提供了极高的法源压缩比和速度。

       2. LZMA2算法：这是原理LZMA算法的进一步优化版本，它在LZMA的算算法基础上，引入了额外的法源压缩策略，以提高压缩效果和效率。原理

       3. PPMD算法：该算法基于Dmitry Shkarin的算算法PPMdH算法，它采用基于概率的法源预测技术，通过预测文件内容来实现高效的原理压缩。

       4. BCJ算法：这是针对位x可执行文件的转换程序，它能够将可执行文件进行压缩，以减小文件大小，提高传输和存储效率。

       5. BCJ2算法：与BCJ算法类似，它也是针对位x可执行文件的优化压缩技术，进一步提高了BCJ算法的压缩效率和效果。

       6. BZip2算法：这是基于标准的BWT算法，它通过使用可变长度的编码方式，对文件进行压缩，以达到较高的压缩比。

       7-Zip的网站模板源码克隆算法选择可以根据文件类型和压缩需求进行优化，例如对于文本文件和程序代码，LZMA和PPMD算法通常效果较好；而对于二进制文件，BCJ和BZip2可能更为合适。7-Zip的开放结构和兼容性使其成为多种压缩、转换、加密算法的高效整合平台，支持的文件容量上限也达到了惊人的,,, GB，以Unicode为标准的文件名和对固实压缩、文件头压缩的支持，使得7-Zip在文件管理方面具有高度的灵活性和兼容性。

扩展资料

       7-Zip 软件基于 GNU 次要公共许可协议(Lesser General Public License) 之下发布，是一款完全免费的压缩解压软件。7-Zip是一款免费开源的解压缩软件，命令行选项具有强大的设置功能，非常适合用来备份，将介绍如何操作。将使用没有图形界面的7-Zip，操作通过命令行完成。这样做的好处之一就是整个软件的程序只有一个文件，适合在U盘中随身携带，易于操作。

zip压缩影响画质原理

色彩失真。

       ç”±äºŽZIP压缩算法是基于像素数据的，因此在压缩过程中会导致色彩失真。这主要是因算法在压缩过程中会丢失一些颜色信息，导致压缩后的图像颜色看起来不如原始图像鲜艳。

LZMA压缩与解压原理是什么？

       LZMA压缩与解压：揭秘7zip背后的高效技术

       当提到数据压缩的高效利器，7zip无疑是一个不容忽视的名字。7zip背后的压缩算法LZMA，其核心原理并非单一的LZ那么简单，而是大逃杀游戏 源码结合了多种技术，展现出卓越的压缩性能。LZMA算法的核心策略是:

       它像一位侦探，在数据流或文件中搜索重复出现的字符串，一旦找到，就用一个精妙的编码来标记——一个指向先前出现过相同字符串位置的指针，再加上那段字符串的长度。这种策略显著地减少了数据的存储空间，实现了高效压缩。LZMA算法巧妙地与Huffman编码和Deflate算法联手，Huffman编码用于构建最优的字符编码表，而Deflate算法则在LZMA的基础上进一步提升压缩效果，通过动态调整匹配窗口和编码策略，实现了更出色的压缩性能。

       总的来说，LZMA算法凭借其智能的重复字符串检测和编码机制，就像一场数据压缩的魔术，将冗余的数据转化为紧凑的代码，从而在保证数据完整性的前提下，大大缩减存储空间，是现代数据存储和传输中的瑰宝。无论是文件压缩还是网络传输，LZMA都展现出了其强大而实用的价值。

安装Linux下的LZMA压缩工具linux安装lzma

       LZMA是7Zip开发的主要压缩算法，它可以比其他算法生成更小的文件和更高的压缩率。安装LZMA的Linux环境有许多优势，包括减小文件体积、平均股价公式源码减轻存储负担和节省计算资源。本文将介绍Linux环境中安装LZMA的步骤以及在实践中的使用经验。

       一、安装LZMA压缩工具

       1. 检查系统中是否已安装LZMA

       检查系统中是否已安装LZMA：

       > whereis lzma

       如果现有系统没有安装LZMA，则需要进行安装，可以使用源码包、二进制包或者包管理器进行。

       2. 安装LZMA源码包

       获取LZMA源码包:

       > wget pression software）自然就是利用压缩原理压缩数据的工具，压缩后所生成的文件称为压缩包（archive），体积只有原来的几分之一甚至更小。当然，压缩包已经是另一种文件格式了，如果你想使用其中的数据，首先得用压缩软件把数据还原，这个过程称作解压缩。常见的压缩软件有winzip、winrar等

[译] 理解 zip 和 gzip 压缩格式背后的压缩算法

       众所周知，在网络传输数据时，每个字节都需要占用流量，这意味着需要支付费用。尽管存在多种压缩算法，但zip算法可能是最流行的。gzip算法虽然与zip同名，但却是另一种不同的算法。gzip算法在HTTP协议中也得到了广泛应用。尽管各种压缩算法适用于不同场景，但它们的底层都是基于DEFLATE算法。DEFLATE是一种结合了LZ算法和哈夫曼编码的无损数据压缩算法。

       LZ算法是一种用于文本压缩的无损压缩技术。该算法通过使用编码器或解码器中已经出现过的匹配数据信息来替换当前数据，从而实现压缩功能。

       LZ算法并非在整个文本中同时查找重复的字母，而是首先设置一个固定大小的搜索缓冲区，例如（在实际场景中，这个缓冲区的微募捐系统源码大小通常是几十KB）。在逐一对文本中的字母进行编码时，首先会判断当前字母是否出现在前面缓冲区的个字母中。如果能找到匹配的字母，就记录下当前字母与找到的字母的偏移量d，这样就完成了一个字母编码的第一阶段。接下来，用当前在编码字母邻近的下一个字母与缓冲区中匹配上字母邻近的下一字母进行匹配，如果匹配上就继续进行下一个字母的匹配，如此循环往复，直到缓冲区个字母匹配完或者邻近的字母未匹配上，就结束匹配过程。完成上述过程后，将当前位置匹配上的连续字母替换成与缓冲区字母的偏移量以及这段连续字母的个数l。这样，字母编码的第二阶段就完成了。

       让我们用一个例子来看看它是如何工作的：

       首先，最简单的方法就是直接替换第二次出现的O为指向第一次出现的O的一个标记，或者替换第二次出现的RTO为指向第一次出现的RTO。

       下面更具体地描述一下这个过程。假定我们设置的缓冲区大小是4，把这4个长度的缓冲区看成是一个滑动窗口沿着正文文本向右滑动：

       滑动窗口随着编码的迭代一步步向右移动，前面4步中滑动窗口内的字母都没有发现重复。到了第5步，滑动窗口内字母O已经出现重复了，然后查看字母O右侧的R，发现滑动窗口中匹配字母O右侧相邻的字母并非R，便不再继续向右进行匹配，将第2个O替换成(1, 1)（表示：滑动窗口中匹配的字母离当前字母偏移距离为1，匹配上的连续字母长度为1）。在第6步中，滑动窗口中字母R与其左边第4个字母匹配上了，继续检查下一个字母T的匹配情况，然后发现滑动窗口中RT也匹配上了。然后继续下一个字母O，在滑动窗口中匹配RTO也匹配上了，并且到此为止，因为下一个字母匹配上了。滑动窗口中匹配上的字母与当前字母的偏移距离为4，同时有连续3个字母匹配上了，所以这里将匹配上的3个字母替换成(4, 3)。接着在第7步中，字母R与偏移距离3出的字母匹配上，但是接下来的RR并未匹配上，在第8步中发现最近的匹配上的R的偏移距离为1。最终整段文本经过编码的结果如下：

       压缩过的文本其实是由一系列的这种(d, 1)标记对和字母组成，标记对无法直接找到相匹配的字母。在解压过程中，字母保持不变，这种标记对转换为其指向位置的字母。下面看一个解压的例子：

       字母abc保持不变，标记对(3, 2)表示从当前位置向左移动3个单位，然后取出2个字母，因此其转换为ab。现在原始文本变成了这样abcab(1, 1)，最后一个标记对表示从当前位置向左移动1个单位，然后取出1个字母，因此转换为b。最终解压完成的文本为abcabb。

       在用LZ消除文本中重复的字母后，再使用哈夫曼编码进行第二次压缩。这种方法用较短的编码代替较常用的字母，用较长的编码代替较少用的字母，从而减少了文本的总长度。

       让我们用一个简单的示例文本来看看它是如何工作的。

       这个例子中，我们希望能无损地压缩这段文本。通常一个字母占用8字节，所以这段文本总长度有字节。在这段文本中，我们发现其中字母F只出现了1次，而字母E出现了7次。哈夫曼编码正是利用了这一特性，通过减少出现频率高的字母本身的字节长度，来减少整个文本所占的总长度。

       要采用哈夫曼编码压缩文章，首先需要统计各个文本中各个字母的出现频率。上述例子中的字母频率如下：

       我们需要使用文本中的字母作为叶子节点来构建一颗二叉树，通过这棵二叉树来编码文本中的每一个字母。从出现频率最小的字母：P和F开始，让其作为底层的叶子节点，将其频率相加的值作为父节点，这样便得到了如下的二叉树：

       重复上面的步骤，依次使用频率最小的字母：U和O以及R和T，最后剩下频率最高的字母E先单独放着。

       接下来使用上面得到的4个二叉树作为子节点来创建一颗更大的二叉树，将上面的二叉树的根节点的频率值递增排序，优先使用根节点频率值小的二叉树作为新的二叉树子节点。这里使用U和O、R和T这组二叉树组成了如下的一颗二叉树：

       这时候还有3颗二叉树，根节点分别为：9、9、7（第一个9是上一步创建的二叉树），同样的，将根节点频率值最小的两个作为子节点创建新的二叉树如下：

       现在剩下一颗将根节点值为的大二叉树和根节点值为9叶子节点为R、T的二叉树，将其作为子节点创建一颗新的二叉树如下：

       现在我们要做的就是根据这棵二叉树来对文本进行编码。依次从跟节点访问各个字母，遇到左分支当成0，遇到右分支当成1，按照字母沿着二叉树访问路径的顺序所将这些0、1连接起来。比如，从根节点到字母E先后需要经过1次左分支和1次右分支，所以字母E的编码为。字母U需要经过4次左分支，其编码为；F需要经过2次左分支和2次右分支，其编码为。可以发现，在这里例子中出现频率非常高的字母E编码后位数比出现频率较少的字母F编码后位数要少。经过这样的编码处理，最终压缩过的文本如下：

       这段压缩后的文本长度只有位，远比原始的位长度小。

       假如收到这样一段压缩过的文本，我们希望能够解压它让其变得可以理解。我们都知道一段未压缩过的文本中的一个字符占用8位，上面说过经过哈夫曼编码压缩后一个字符的位数并不是固定8位的，所以并不清楚一段数据（比如：）是表示1个字符、2个字符或者3个字符，因此这段压缩过的文本将如何解压呢？

       这一步不存在任何奇迹，要准确解压还需要上面编码中构建的二叉树。得到这个用于编码的二叉树有两种方案，第一种是其和压缩后的文本放一起作为原始文本的压缩结果，这可能会导致压缩后的文本比原始文本还要大；第二种方案是使用预先定义好的二叉树。我们知道各个字母在英语中的使用频率，完全可以根据这个频率来构建上述的二叉树。使用这种预先定义的公共字母频率二叉树压缩部分文本的结果可能比根据文本内容字母频率二叉树压缩的效果差一些，但是这样不再需要将字母频率二叉树保存到压缩后的文件中。总而言之，这两种方案各有优缺点。

       虽然本文没有深入的分析各种压缩算法原理的细节和对应的实现，但是经过上述讲解你应该已经对文本如何被压缩成zip和gzip等格式有了大概的认识。希望本文能满足你对压缩算法神秘面纱的好奇心：）

       *从技术上来说，zip压缩格式是支持使用其他的压缩算法的，但是DEFLATE是其中最常用的一种。

       如果发现译文存在错误或其他需要改进的地方，欢迎到掘金翻译计划对译文进行修改并PR，也可获得相应奖励积分。文章开头的本文永久链接即为本文在GitHub上的MarkDown链接。

       掘金翻译计划是一个翻译优质互联网技术文章的社区，文章来源为掘金上的英文分享文章。内容覆盖Android、iOS、前端、后端、区块链、产品、设计、人工智能等领域，想要查看更多优质译文请持续关注掘金翻译计划、官方微博、知乎专栏。