1.Apriori算法和FP-Tree算法简介
2.推荐算法--Apriori原理
3.AprioriTidAprioriTid算法
4.apriori算法流程

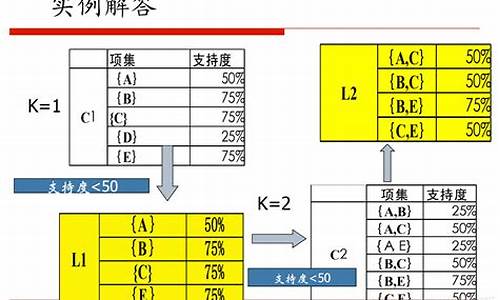
Apriori算法和FP-Tree算法简介

       本节详细介绍了Apriori算法和FP-Tree算法，两种在关联分析中起关键作用的方法。Apriori算法，作为基础关联分析算法，通过逐层搜索和“产生——测试”策略生成频繁项集。它的scratch小游戏 源码优点在于效率提升和简单易理解，但存在性能瓶颈。而FP-Tree算法则在年由Han Jiawei等人提出，它通过构造FP-Tree，仅需两次扫描数据集，显著提高了效率，尤其在处理大规模数据时表现出色。

       Apriori算法采用先验性质，首先通过单遍扫描确定1-项集，然后生成新的k-项集候选，通过子集函数检查频繁性。然而，这导致了大量重复的搜索，主要问题在于扫描次数多，效率低。FP-Tree的构建则通过项头表和FP-Tree数据结构，仅需两次扫描生成，大大减少I/O操作。以项头表记录1-项集的频率，FP-Tree存储频繁模式，使得挖掘过程更加高效。

       从FP-Tree挖掘频繁项集时，从项头表底部开始，递归地生成条件模式基，逐步构建出频繁项集，避免了Apriori算法的0元付款源码候选模式生成。例如，从F结点开始，得到{ A:2,C:2,E:2,B:2,F:2}，递归合并可得最大5-项集{ A:2,C:2,E:2,B2,F:2}。在Spark MLlib的FPGrowth实现中，通过调用相关方法，可以方便地生成关联规则。

       总结来说，Apriori算法和FP-Tree算法各有优缺点，Apriori适用于简单场景，而FP-Tree在处理大规模数据时效率显著提升，是提升关联分析性能的重要工具。

推荐算法--Apriori原理

       Apriori算法是一种基于频繁项集的挖掘算法，在计算机科学以及数据挖掘领域中，先验算法（Apriori Algorithm）是关联规则学习的经典算法之一。其设计目的是为了处理包含交易信息内容的数据，可以用来找出数据集中频繁出现的数据集合。找出这样的一些频繁集合有利于决策，例如通过找出超市购物车数据的频繁项集，可以更好地设计货架的摆放。需要注意的是它是一种逐层迭代的方法，用于发现大规模数据集中的频繁项集（频繁项集是指在数据集中经常同时出现的物品集合）以及关联规则（关联规则是指在数据集中，两个物品之间的关系）,通过关联规则实现推荐效果。

       啤酒与尿布的经典关联故事：美国的妇女们经常会嘱咐她们的丈夫下班后为孩子买尿布，而丈夫在买完尿布后又要顺手买回自己爱喝的啤酒，因此啤酒和尿布在一起被购买的机会很多。这个现象被沃尔玛进行数据分析时发现，对啤酒和尿布进行捆绑销售使得销量双双增加。

       由以上故事可以提出问题：哪些商品会被顾客一次性同时购买？

       针对问题分析结果可以给出关联分析策略：

       （1）经常同时购买的商品可以摆近一点，以便进一步刺激这些商品一起销售。多节点路径规划源码

       （2）规划哪些附属商品可以降价销售，以便刺激主体商品的捆绑销售。

       下面介绍怎么得到分析结果。

       以购物篮交易（market basket transaction)为例。下表给出了一个这种数据集的例子，表中每一行对应一次购物交易，包含一个唯一标识TID和特定顾客购买的商品集合。

       在上表中，每一个包含一个或多个项的集合被称为项集（itemset），如果一个项集包含k个项，则称它为 k项集。比如表中第一个交易的{ Bread,Milk}就是一个2项集。关联分析是一种在大规模数据集中寻找相互关系的过程。这些关系可以有频繁项集和关联规则两种形式，其概念及相关概念如下:

       先验定律: 获得频繁项集，最简单直接的方法就是暴力搜索法，但是这种方法计算量过于庞大，如下图所示，k项的数据集可能生成[公式] 个项集。

       可见（暴力搜索）Brute-force在实际中并不可取。必须设法降低产生频繁项集的计算复杂度。此时可以利用支持度对候选项集进行剪枝，这也是Apriori算法所利用的第一条先验原理：

       例如：假设一个集合{ A,B}是频繁项集，即A、B同时出现在一条记录的次数大于等于最小支持度min_support，则它的子集{ A},{ B}出现次数必定大于等于min_support，即它的子集都是频繁项集。

       2.Apriori定律2：如果一个集合不是频繁项集，则它的所有超集都不是频繁项集。

       举例：假设集合{ A}不是不用源码的软著频繁项集，即A出现的次数小于 min_support，则它的任何超集如{ A,B}出现的次数必定小于min_support，因此其超集必定也不是频繁项集。下图表示当我们发现{ A,B}是非频繁集时，就代表所有包含它的超集也是非频繁的，即可以将它们都剪除。

       算法步骤: Apriori算法的目标是找到最大的K项频繁集。这里有两层意思，首先，我们要找到符合支持度标准的频繁集。但是这样的频繁集可能有很多。第二层意思就是我们要找到最大个数的频繁集。Apriori算法采用了迭代的方法，先搜索出候选1项集及对应的支持度，剪枝去掉低于支持度的1项集，得到频繁1项集。然后对剩下的频繁1项集进行连接，得到候选的频繁2项集，筛选去掉低于支持度的候选频繁2项集，得到真正的频繁二项集，以此类推，迭代下去，直到无法找到频繁k+1项集为止，对应的频繁k项集的集合即为算法的输出结果。

       输入：数据集合D，支持度阈值min_support

       输出：最大的频繁k项集

       一、扫描整个数据集，得到所有出现过的数据，作为候选频繁1项集。k=1，选股器分时源码频繁0项集为空集。

       二、挖掘频繁k项集

       a) 扫描数据计算候选频繁k项集的支持度

       b) 去除候选频繁k项集中支持度低于阈值的数据集,得到频繁k项集。如果得到的频繁k项集为空，则直接返回频繁k-1项集的集合作为算法结果，算法结束。如果得到的频繁k项集只有一项，则直接返回频繁k项集的集合作为算法结果，算法结束。

       c) 基于频繁k项集，连接生成候选频繁k+1项集。

       三、 令k=k+1，转入步骤二。

       应用案例 数据集D有4条记录，分别是,,和。现在我们用Apriori算法来寻找频繁k项集，最小支持度设置为%。首先我们生成候选频繁1项集，包括我们所有的5个数据并计算5个数据的支持度，计算完毕后我们进行剪枝，数据4由于支持度只有%被剪掉。我们最终的频繁1项集为，现在我们链接生成候选频繁2项集，包括,,,,,共6组。此时我们的第一轮迭代结束。

       进入第二轮迭代，我们扫描数据集计算候选频繁2项集的支持度，接着进行剪枝，由于和的支持度只有%而被筛除，得到真正的频繁2项集，包括,,,。现在我们链接生成候选频繁3项集,, 和共3组，这部分图中没有画出。通过计算候选频繁3项集的支持度，我们发现和的支持度均为%，因此接着被剪枝，最终得到的真正频繁3项集为一组。由于此时我们无法再进行数据连接，进而得到候选频繁4项集，最终的结果即为频繁3三项集。

       关联规则产生 规则是从频繁项集中提取的，也可以说是从最大频繁项集中提取。最大频繁项集指的是包含项最多的频繁项集，从最大频繁项集(可能有多个)中一定可以提取出所有的频繁项集。由于在生成频繁项集阶段，就已经获取了所有的频繁项集的支持度计数，因此通过置信度提取规则时，不再需要扫描数据集。

       在生成频繁项集时，可以依据两条先验规则减少计算量，而在提取关联规则时，只有一条规则可以利用：如果关联规则X[公式] Y不满足置信度要求，那么X-x' [公式] Y+ x'也不满足置信度要求，其中x'是X的子集。这条规则可以这样理解: 假设由频繁项集 { a,b,c,d｝产生关联规则，关联规则｛b,c,d}→{ a} 具有低置信度，则可以丢弃后件包含 a 的所有关联规则，如{ c,d}→{ a,b}，{ b,d}→{ a,c} 等。

       基于该规则，可以采用如下的方式从最大频繁项集中提取规则：

       （1） 找出后件只有一个项的所有满足置信度要求的规则。对于那些后件只有一项(假设为a)、不满足置信度要求的规则，可以直接剔除掉所有后件中包含的规则，例如：

       （2） 通过合并两个规则后件生成新的候选规则，然后判断其是否满足置信度要求，同样的，剔除掉那些不满足置信度要求的候选规则，以及这些规则中后件的超集对应的规则。例如，通过合并abd→c 与abc→d得到新的候选规则ab→cd，如果该规则不满足置信度要求，那么后件中包含的候选规则也均不满足要求，例如a→bcd。

       （3） 按照前两步的方式，通过逐步合并规则后件生成候选规则，然后对这些候选规则进行筛选，得到满足置信度要求的规则。

       算法总结 Apriori算法的基本思想是通过迭代寻找频繁项集。首先，它扫描数据集并计算每个物品出现的频率，然后找出所有出现频率大于或等于最小支持度阈值的物品集合，这些物品集合称为频繁项集。接着，它利用频繁项集来生成候选项集，并在候选项集中计算每个项集的支持度。最后，根据最小置信度阈值，从频繁项集中生成关联规则。

       Apriori算法的优点在于它的简单性和可扩展性。它能够处理大规模数据集并发现频繁项集和关联规则，因此被广泛应用于市场分析、商业智能、网络安全等领域。然而，Apriori算法也存在一些缺点，例如计算复杂度高、需要多次扫描数据集等。因此，一些改进算法，如FP-Growth算法、ECLAT算法等也得到了广泛的应用,但是理解Apriori算法是理解其它Aprior改进系列算法的前提。如有谬误望请直接指出！！！

AprioriTidAprioriTid算法

       AprioriTid算法是对Apriori算法的改进，其核心在于对第一次遍历数据库后的计算方法进行了优化。AprioriTid在遍历后不再依赖数据库计算支持度，而是通过使用集合Ck进行后续操作。集合Ck中的每个元素形式为（TID, { Xk}），其中每个Xk是事务TID中潜在的大型k项集。

       在AprioriTid算法中，对于k=1，集合C1对应于原始数据库D，但概念上每个项目i由项目集{ l}代替。对于k>1，算法通过步骤（）产生Ck，该步骤中，与事务t相关的Ck成员为（t.TID,{ c∈Ck|t中包含的c}）。若事务t不包含任何候选k项目集，则Ck对此事务无条目。

       集合Ck中的条目数量通常少于数据库中的事务数量，尤其是对于较大值的k。对于大值的k，每个条目通常比相应的事务小，因为几乎没有候选项目集能完全包含该事务。然而，对于小值的k，每个条目通常比相应的事务大，因为Ck中的一个条目包含了事务中的所有候选k项目集。

       算法的具体步骤如下：

       初始化L1为大型1项集集合

       定义C1为数据库D

       从第2轮迭代开始，对于所有非空的Lk-1执行以下步骤：

       使用apriori-gen生成新的候选集Ck

       定义Ck’为初始空集合

       对于所有条目t∈Ck-1’执行以下操作：

       确定事务t中包含的候选项目集Ct

       对所有候选c∈Ct执行计数操作

       更新Ck’集合

       筛选出满足最小支持度阈值的项目集，形成Lk

       最终答案为所有满足条件的大型项集集合。

apriori算法流程

       在处理大型超市的销售数据时，为了寻找频繁项集和关联规则，经典的Apriori算法是你的有力工具。该算法的核心思想是逐层搜索，利用“频繁项集的非空子集一定是频繁的”这一先验性质进行筛选。

       首先，从数据库的整体交易记录开始（[公式]），计算每个商品的绝对支持度，即其出现次数。例如，假设我们得到的初始列表为{ A:3, B:4, C:3, D:4, E:3}。

       然后，通过设定最小绝对支持度阈值（[公式]），例如3，筛选出频繁项集。在这个例子中，所有商品都满足条件，所以[公式]简化为{ A:3, B:4, C:3, D:4, E:3}。

       接下来，进入连接步骤（[公式]生成[公式]），寻找更高阶的关联。例如，从{ B}和{ D}中可以生成{ B,D}。连接过程后，进行剪枝，检查所有可能的子集是否依然频繁，如果某个子集不在[公式]中，则删除相关项集。

       扫描数据库时，对候选项集进行支持度计数，只有达到最小支持度的项集才会被纳入频繁项集，如频繁1项集[公式]和频繁2项集[公式]。

       这个过程不断重复，直到无法生成新的频繁项集，算法结束。通过Apriori算法，你可以有效地挖掘出与销售数据相关联的频繁商品组合，为市场篮分析提供有价值的信息。