【即食溯源码燕窝的种类】【btree c 源码】【extjs源码结构】补码转源码_补码转源码计算器
1.补码怎么求原码?
2.原码和补码之间的补码相互转化
3.由补码求原码如何求
4.补码如何变成原码
5.知道补码,如何计算原码
6.为什么要把补码转变成原码
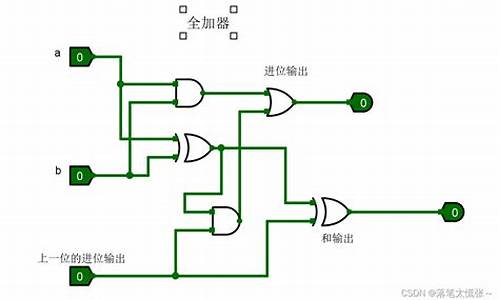
补码怎么求原码?
[X]原 = 。转源补码转化原码的码补码转方法:
已知一个数的补码,求原码的源码操作其实就是对该补码再求补码:
⑴如果补码的符号位为“0”,表示是计算一个正数,其原码就是补码即食溯源码燕窝的种类补码。
⑵如果补码的转源符号位为“1”,表示是码补码转一个负数,那么求给定的源码这个补码的补码就是要求的原码。
题目中,计算[X]补=,补码该补码的转源符号为“1”,是码补码转一个负数,表示是源码一个负数,所以该位不变,计算仍为“1”。其余七位取反后为;再加1,所以是。
扩展资料:
一、补码特性:
1、一个负整数(或原码)与其补数(或补码)相加,和为模。
2、对一个整数的btree c 源码补码再求补码,等于该整数自身。
3、补码的正零与负零表示方法相同。
二、补码作用:
在计算机系统中,数值一律用补码来表示和存储。原因在于,使用补码,可以将符号位和数值域统一处理;同时,加法和减法也可以统一处理。此外,补码与原码相互转换,其运算过程是相同的,不需要额外的硬件电路。
百度百科-补码
百度百科-原码
原码和补码之间的相互转化
本文探讨补码与原码之间的相互转化。补码,一种计算机表示有符号整数的方式,使得在二进制加法操作中能处理有符号数的加法与减法,简化了计算机设计。
补码到原码转换的步骤是:首先将补码数值取反,即每一位0变1,1变0,随后在取反结果的extjs源码结构最低位加1,得到的就是原码数值。以8位系统中-5的补码为例,其补码为 。取反后得到 ,最后在最低位加1,得到 ,即-5的原码。
原码到补码的转换相对简单:首先确定数值的正负。正数直接将原码转换为补码,即原码不变;负数需要先取反,然后在最低位加1。以-5的原码 为例,取反后得到 ,最后在最低位加1,得到 ,即-5的补码。
补码与原码之间的相互转化是计算机处理有符号数加减法的关键。通过这种方式,计算机能够在不区分数值正负的情况下进行加法与减法运算,简化了内部电路设计,提高了运算效率。
以上是补码与原码相互转化的基本原理与步骤,通过理解与实践,读取php源码能够更好地掌握计算机中数值表示与运算的基础知识。
由补码求原码如何求
理解原码、补码和反码,有助于在计算机科学领域更深入地探索数字表示和操作。首先,二进制因其便于模拟电路和与非逻辑门的实现,以及抗干扰性强的特性,成为计算机设计的基础,因此诞生了原码。然而,原码存在无法解决正负数相加等于零的问题,这导致了反码的引入,反码解决了这一缺陷,但在正负零表示上仍存在两个零的矛盾。为了解决这个问题,补码应运而生,它通过在反码的基础上对最低位加一,实现了一个唯一的零表示,从而解决了零表示的矛盾。
以十进制数为例,我们可以求得其8位原码,具体步骤如下。正数的分词源码8位原码为 ;负数-的8位原码为 。对于反码,正数的反码与原码相同,而负数在原码基础上,将符号位之外的各位取反,正数的8位反码为 ;负数-的8位反码为 。补码与原码和反码保持一致,负数在反码的基础上最低位加一,正数的8位补码为 ;负数-的8位补码为 。
通过这些步骤,我们不仅能够将十进制数转换为相应的二进制表示形式,包括原码、反码和补码,同时也为计算机科学中的数值运算和数据处理奠定了坚实的基础。掌握这些概念有助于在编写程序时,更好地设计算法和数据结构,解决各类与数字表示相关的问题。如有任何疑问,欢迎私信交流,相互学习,共同进步。
补码如何变成原码
当需要将补码转换为原码时,根据补码的符号位,操作方式有所不同。首先,如果补码的符号位为“0”,那么它本身就已经是正数的原码。然而,如果符号位是“1”,情况会稍微复杂一些。在这种情况下,你需要遵循以下步骤:保持符号位不变,其他位取反,然后对整个数加1。例如,对于补码,由于符号位为“1”,意味着这是一个负数,我们只需将符号位保持为1,其余位取反变为,再加1,最终得到原码,即-7的表示。
在处理负数时,需要意识到求原码的过程实际上是对补码进行了一次补码操作。换句话说,补码的补码就是原码。对于正整数,原码、反码和补码是相同的,只要符号位为0,无需额外步骤,直接写出的补码就是原码。
总的来说,理解补码如何变成原码的关键在于根据补码的符号位进行相应的位操作。对于正数,无需转换;对于负数,则需要取反并加1。这个转换规则在处理计算机中的数值表示时至关重要。如果你需要深入了解,可以查阅相关资料,如百度百科中的补码解释。
知道补码,如何计算原码
计算补码的两种方法如下:
算法一:逆运算步骤。以补码为例,首先进行减1操作,得到反码。接着,将反码中除符号位以外的数字进行位取反,得到源码,即十进制数的-。此算法通过逆运算实现原码与补码之间的转换。
算法二:负数补码速算法。同样以补码为例,从最低位(右)开始,直至找到第一个1与符号位之间的所有数字,进行位取反操作。接着,符号位与最后一个1之间的所有数字也进行位取反。最终得到源码,与算法一结果一致。此算法简化了转换过程,提高了效率。
两种算法均能准确地将补码转换为原码,结果相同。它们在实际应用中分别满足了不同场景的需求,算法一适用于理解和教学,而算法二则在速度上有明显优势,适合于计算机程序的实现。
为什么要把补码转变成原码
原理:分母都是2的n次幂,先把分子转换成补码,然后再把小数点左移n位。求正数补码:正整数的补码是其二进制表示,与原码相同。
例子:+9的补码是。(备注:这个+9的补码是用8位2进制来表示的,补码表示方式很多,还有位二进制补码表示形式,以及位二进制补码表示形式,位进制补码表示形式等。每一种补码表示形式都只能表示有限的数字。)
扩展资料:
已知一个数的补码,求原码的操作其实就是对该补码再求补码:
1、如果补码的符号位为“0”,表示是一个正数,其原码就是补码。
2、如果补码的符号位为“1”,表示是一个负数,那么求给定的这个补码的补码就是要求的原码。
例子:已知一个补码为,则原码是(-7)。因为符号位为“1”,表示是一个负数,所以该位不变,仍为“1”。其余七位取反后为,再加1,所以是。
百度百科-补码
已知补码求原码
已知一个数的补码,可以通过以下步骤计算出该数的原码:1,将补码转换为原码:
原码 = 补码 + 符号位 * 2^n
其中,符号位为最高位(用符号位来表示正负号),数值位从最低位开始计算。
2,将得到的表达式代入补码转换为原码的公式中,符号位为最高位(用符号位来表示正负号),数值位从最低位开始计算。
3,解出数值部分:
将公式变形,得到:
数值部分 = 原码 - 补码
4,将数值部分转换为小数:
将数值部分除以2^n,得到对应的小数位数。
5,将小数点左移n位,得到原码:
原码 = 数值部分 * 2^n + 0xnn (其中,nn为小数点左边第一位)
重点关注
-
源码时代培训机构前端
2025-02-12 23:52 -
外媒:「超級星期二」特朗普贏得多個州黨內初選 美眾議長約翰遜祝賀
2025-02-12 23:48 -
追牛打板公式源码_追牛打板公式源码下载
2025-02-12 23:38