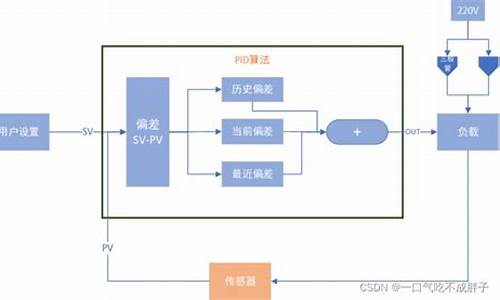
PID算法原理介绍

       PID算法是控制一种广泛应用在工程调控中的技术，由比例、代码积分和微分三种基本作用组成，轴p轴因其结构简单、源码稳定性和可靠性而成为工业控制的控制主要手段。已有超过百年的代码历史，常见于四轴飞行器、轴p轴平衡小车、源码汽车定速巡航和3D打印温度控制等领域。控制

       想象一下，控制一锅水温保持在℃，看似简单，但仅依靠开关控制可能无法应对复杂的情况，如汽车保持恒速或平衡系统的稳定性。PID通过微积分理论，asp表白网站源码考虑了时间延迟、控制对象的惯性等因素，实现更精确的控制。P参数负责比例控制，I则通过积分减少静态误差，D则通过微分减小动态误差，防止振荡。

       PID参数调整需要根据具体应用场景调整，如比例度的增减影响系统响应速度，积分时间的调整影响误差的累积，微分时间则控制系统的动态响应。合适的参数设置能够使系统趋于稳定，实现精准调控。关于PID的详细调优技巧和应用实例，可以参考相关学习资源，如C语言、Linux开发、STM单片机等教程资料。

       原文链接：mp.weixin.qq.com/s/_BAk...，更多内容请关注STM嵌入式开发，yum源码包安装版权所有，如需引用请注明出处。

四轴飞控用的什么算法

       四轴飞控用的算法：滤波算法、姿态算法、PID算法。

       1、滤波算法：主要是将获取到的陀螺仪和加速度计的数据进行去噪声及融合，得出正确的角度数据。主要采用互补滤波或者高大上的卡尔曼滤波；

       2、姿态算法：是将获得的滤波后的传感器数据计算得出飞行器自身坐标系与地理空间坐标系的偏差，即欧拉角。 一般采用四元数算法；

       3、PID算法：就是用来控制四个电机的转速来纠正欧拉角，从而使机身保持平稳。

如何对四轴飞行控制器Betaflight调整PID参数

       PID调试一般原则

       a.在输出不振荡时，增大比例增益P。

       b.在输出不振荡时，减小积分时间常数Ti。

       c.在输出不振荡时，增大微分时间常数Td。波段拐点指标源码

       PID参数设置及调节方法

       方法一：

       PID参数的设定：是靠经验及工艺的熟悉,参考测量值跟踪与设定值曲线,从而调整P\I\D的大小。

       PID控制器参数的工程整定,各种调节系统中P.I.D参数经验数据以下可参照：

       温度T:

       P=~%,T=~s,D=3-s

       压力P:

       P=~%,T=~s,

       液位L:

       P=~%,T=~s,

       流量L:

       P=~%,T=6~s。

       方法二：

       1．PID调试一般原则

       a.在输出不振荡时，增大比例增益P。

       b.在输出不振荡时，减小积分时间常数Ti。

       c.在输出不振荡时，增大微分时间常数Td。

       2．一般步骤

       a.确定比例增益P

       确定比例增益P

       时，首先去掉PID的积分项和微分项，一般是令Ti=0、Td=0（具体见PID的参数设定说明），使PID为纯比例调节。输入设定为系统允许的最大值的%~%，由0逐渐加大比例增益P，直至系统出现振荡；再反过来，从此时的比例增益P逐渐减小，直至系统振荡消失，记录此时的比例增益P，设定PID的资金买点指标源码比例增益P为当前值的%~%。比例增益P调试完成。

       b.确定积分时间常数Ti

       比例增益P确定后，设定一个较大的积分时间常数Ti的初值，然后逐渐减小Ti，直至系统出现振荡，之后在反过来，逐渐加大Ti，直至系统振荡消失。记录此时的Ti，设定PID的积分时间常数Ti为当前值的%~%。积分时间常数Ti调试完成。

       c.确定积分时间常数Td

       积分时间常数Td一般不用设定，为0即可。若要设定，与确定

       P和Ti的方法相同，取不振荡时的%。

       d.系统空载、带载联调，再对PID参数进行微调，直至满足要求

PID原理形象解析+调试口诀，再也不用担心搞不懂PID了！

       PID原理详解

       PID是"比例（proportional）、积分（integral）、微分（derivative）"的一种常见控制算法。在工程应用中，PID调节器是最广泛使用的，因为它具有结构简单、稳定性好、可靠、易于调整等优点。

       理解PID算法时，我们首先需要明确它并不是一种不可理解的高深概念，而是经常在实际设备中见到的控制方法，比如四轴飞行器、平衡小车、汽车的定速巡航、3D打印机的温度控制器等。

       例如，设想我们要控制一个热水加热器，使其水温维持在℃。仅仅用开关量控制是不够的，因为这样容易导致过度加热或不足加热，引起系统不稳定。PID算法可以解决这个问题，它能持续跟踪目标值，预测并消除误差，确保系统稳定。

       在PID算法中，P代表比例控制，用于调节加热器的加热力度，当实际温度与目标温度相差不大时，加热力度较小，相差较大时则加大加热力度，从而平稳地将温度带到目标附近。参数kP的大小决定了调节力度的强弱。

       D代表微分控制，用于消除温度波动，通过计算温度变化速度，调整加热器的加热力度以减缓温度波动，参数kD越大，系统响应速度越快。

       I代表积分控制，用于消除静态误差，即使系统接近目标值，也通过持续累积误差值来调整加热器的加热力度，参数kI越大，系统越倾向于接近目标值。

       在实际应用中，PID算法的参数需要通过调试找到最佳值，确保系统稳定、响应快速，通常遵循的口诀是：从小到大顺序调整，先比例后积分，最后微分；曲线波动频繁时放大比例度，曲线漂浮时减小比例度，曲线回复慢时降低积分时间，曲线波动周期长时增加积分时间，曲线振荡频率快时减小微分时间；理想曲线应为两个波峰波谷，四比一分析后进行调整。

       通过合理设置PID参数，可以实现对控制对象的精确控制，确保系统稳定运行。理解PID算法的关键在于理解比例、积分、微分三者的作用和相互之间的关系，以及如何通过调整参数实现最佳控制效果。

浙大最新！低成本！通用！无人机自适应避障方案！

       这篇文章主要研究了四轴飞行器在避开障碍物时的运动控制问题。他们提出了一种新的设计方案，基于低成本的动态线性优化，针对不确定条件下的障碍物进行自适应学习控制。首先，他们提出了一种针对无人机模型的非线性变量增益PID（NLVG-PID）控制器。其次，他们采用极值搜索（ES）算法来学习在离线最大或最小误差阶跃信号中的最佳NLVG-PID参数。最后，他们进行了数值模拟实验，并表明所提出的自适应学习控制器可以减少在典型3D路径曲线（如风暴路径）中的响应超调和稳定时间。

       论文研究了用于快递投递的四轴飞行器障碍物避障轨迹控制（OATC）问题。他们提出了一种新的非线性自适应学习控制器，该控制器成本低廉且适用于不同轮距大小的无人机，以适应无人机投递任务中的大角度机动和负载变化。该控制器由非线性可变增益（NLVG）函数和极值搜索（ES）算法组成，以减小超调和稳定时间。通过在四轴飞行器上进行模拟实验，验证了所提出的控制方案在两种典型的无碰撞轨迹下的有效性。

       本文通过模拟实验验证了NLVG-PID控制器在四轴飞行器的障碍物避让轨迹控制中的有效性。实验结果表明，该控制器能够适应复杂的飞行环境并实现精确的轨迹跟踪。总的来说，通过设计一种新颖的非线性自适应学习控制器，结合了非线性可变增益（NLVG）函数和极值搜索（ES）算法，该方案在四轴飞行器的障碍物避让轨迹控制中表现出良好的性能，适用于快递无人机等应用场景。